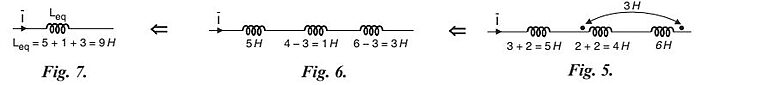Question 5.22: Determine the effective inductance of the series-connected c......
Determine the effective inductance of the series-connected coupled coils shown in Figs 1, 2 and 3.

Learn more on how do we answer questions.
a) To find the equivalent inductance of series-connected coils in Fig. 1
Consider the series-connected coils shown in Fig. 1. There are two mutual couplings. Let us remove them one by one.
Let \overline{I} be the current through the series-connected coils as shown in Fig. 4.
The coupling between 3 H and 2 H coils is additive because the current \overline{I} enters at the dotted end in both the coils. Hence, the magnetic coupling is eliminated by adding the mutual inductance 2 H to the self-inductances as shown in Fig. 5.
The coupling between 4 H and 6 H coil of Fig. 5 is opposive, because the current \overline{I} enters at the dotted end in one coil and leaves at the dotted end in the other coil. Hence, the magnetic coupling is eliminated by subtracting the mutual inductance 3 H from the self-inductances as shown in Fig. 6.
Now, the series-connected inductances of Fig. 6 can be added to give an equivalent inductance as shown in Fig. 7.
b) To find the equivalent inductance of series-connected coils in Fig. 2
In Fig. 2, there are two mutual couplings. Let us remove them one by one as shown below:Let \overline{I} be the current through the series combination as shown in Fig. 8. Here both the couplings are opposive because the current enters at the dotted end in one coil and leaves at the dotted end in the other coil.
c) To find the equivalent inductance of series-connected coils in Fig. 3
In Fig. 3, there are three mutual couplings. Let us remove them one by one as shown below: Let \overline{I} be the current through the series combination as shown in Fig. 9. Here all the couplings are
opposive because the current enters at the dotted end in one coil and leaves at the dotted end in the other coil.
Alternate Method
Alternatively, the magnetic coupling in two series-connected coils can be represented by an additional inductance of value +2M or −2M in series with the coils.
When current enters (or leaves) at the dotted ends in both the coils, the flux is aiding and so it is represented by an additional inductance of +2M in series with the coils.
When current enters at the dotted end in one coil and leaves at the dotted end in other coil, the flux is opposing and so it is represented by an additional inductance of −2M in series with the coils.
The estimation of equivalent inductance of the series-connected coils by this method is illustrated diagrammatically here.