Question 5.25: Determine the equivalent impedance of the parallel-connected......
Determine the equivalent impedance of the parallel-connected impedance with magnetic coupling shown in Fig. 1.

Learn more on how do we answer questions.
Let us assume the current through parallel arms as \overline{I}_{A} \text { and } \overline{ I }_{B} as shown in Fig. 2. Now the current enters at the dotted end in both the coils. Hence, the connection is parallel aiding.
The magnetic coupling in parallel aiding can be represented as shown in Fig. 3.
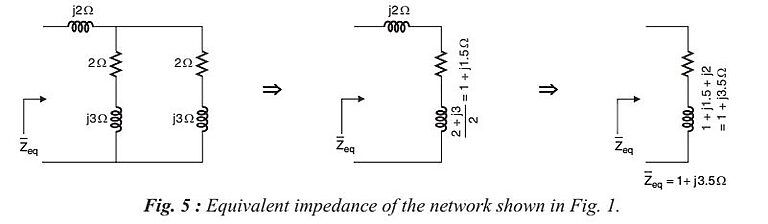
Hence, the network of Fig. 1 can be redrawn as shown in Fig. 4.
The equivalent impedance can be obtained by reducing the network of Fig. 4 to a single equivalent impedance as shown below:
Alternate Method
Let us connect a sinusoidal voltage source of value \overline{E} as shown in Fig. 6. Let, \overline{I}_{1} \text { and } \overline{ I }_{2} be the mesh currents as shown in Fig. 6.
Now, Equivalent impedance, \bar{Z}_{\text {eq }}=\frac{\bar{E}}{\bar{I}_1}
Let us name the coils as coil-A and coil-B. Now the current through coil-A is \bar{I}_1-\bar{I}_2 and the current through coil-B is {\bar{I}_2.}
The current \bar{I}_1-\bar{I}_2 flowing in coil-A will induce an \text { emf j2 }\left(\overline{I}_1-\overline{ I }_2\right) in coil-B. Since \bar{I}_1-\bar{I}_2 enters at the dotted end in coil-A, the sign of this emf will be positive at the dotted end in coil-B.
The current \bar{I}_2 flowing in coil-B will induce an \text { emf j2} \overline{I}_2 in coil-A. Since \overline{ I }_2 enters at the dotted end in coil-B, the sign of this induced emf will be positive at the dotted end in coil-A.
The self- and mutual induced emfs in the coils are shown in Fig. 7.
By KVL in mesh-1,
\begin{aligned} &2\left(\overline{ I }_1-\overline{ I }_2\right)+ j 5\left(\overline{ I }_1-\overline{ I }_2\right)+ j 2 \overline{ I }_2=\overline{ E }\\ &\therefore(2+ j 5) \overline{ I }_1+(-2- j 3) \overline{ I }_2=\overline{ E } \end{aligned} ………(1)
By KVL in mesh-2,
\begin{aligned} &2 \bar{I}_2+ j 5 \bar{I}_2+ j 2\left(\bar{I}_1-\bar{I}_2\right)= j 5\left(\bar{I}_1-\bar{I}_2\right)+ j 2 \overline{ I }_2+2\left(\bar{I}_1-\bar{I}_2\right)\\ &\therefore(-2- j 3) \overline{ I }_1+(4+ j 6) \overline{ I }_2=0 \end{aligned} ……..(2)
On arranging equations (1) and (2) in matrix form, we get,
\left[\begin{array}{rr} 2+ j 5 & -2- j 3 \\ -2- j 3 & 4+ j 6 \end{array}\right]\left[\begin{array}{l} \bar{I}_1 \\ \bar{I}_2 \end{array}\right]=\left[\begin{array}{l} \overline{ E } \\ 0 \end{array}\right]
\text { Now, } \Delta_1=\left|\begin{array}{rr} \bar{E} & -2-j 3 \\ 0 & 4+j 6 \end{array}\right|=\bar{E} \times(4+j 6)-0=(4+j 6) \bar{E}
\Delta=\left|\begin{array}{rr} 2+j 5 & -2-j 3 \\ -2-j 3 & 4+j 6 \end{array}\right|=(2+j 5) \times(4+j 6)-(-2-j 3)^2=-17+j 20
\overline{ I }_1=\frac{\Delta_1}{\Delta}=\frac{(4+ j 6) \overline{ E }}{-17+ j 20} \Rightarrow \frac{\overline{ E }}{\overline{ I }_1}=\frac{-17+ j 20}{4+ j 6}
\therefore \overline{ Z }_{ eq }=\frac{\overline{ E }}{\overline{ I }_1}=\frac{-17+ j 20}{4+ j 6}=1+ j 3.5 \Omega