Question F15.5: Determine the minimum dimension b to the nearest mm of the b......
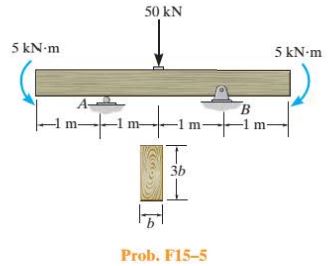
Determine the minimum dimension b to the nearest \mathrm{mm} of the beam’s cross section to safely support the load. The wood has an allowable normal stress of \sigma_{\text {allow }}=12 \mathrm{MPa} and an allowable shear stress of \tau_{\text {allow }}=1.5 \mathrm{MPa}.
At the supports,
V_{\max }=25 \mathrm{kN}
At the center,
M_{\max }=20 \mathrm{kN} \cdot \mathrm{m}
I=\frac{1}{12}(b)(3 b)^{3}=2.25 b^{4}
\sigma_{\text {allow }}=\frac{M_{\max } c}{I} ; \quad 12\left(10^{6}\right)=\frac{20\left(10^{3}\right)(1.5 b)}{2.25 b^{4}}
b=0.1036 \mathrm{~m}=103.6 \mathrm{~mm}
Use b=104 \mathrm{~mm}
I=2.25\left(0.104^{4}\right)=0.2632\left(10^{-3}\right) \mathrm{m}^{4}
Top half of rectangle,
Q_{\max }=0.75(0.104)[1.5(0.104)(0.104)]=1.2655\left(10^{-3}\right) \mathrm{m}^{3}
\begin{aligned} \tau_{\max } & =\frac{V_{\max } Q_{\max }}{I t}=\frac{25\left(10^{3}\right)\left[1.2655\left(10^{-3}\right)\right]}{\left[0.2632\left(10^{-3}\right)\right](0.104)} \\ & =1.156 \mathrm{MPa}<\tau_{\text {allow }}=1.5 \mathrm{MPa} (\mathrm{OK}) .\end{aligned}