Question 5.9: Determine the normal modes of vibration of the symmetric lin......
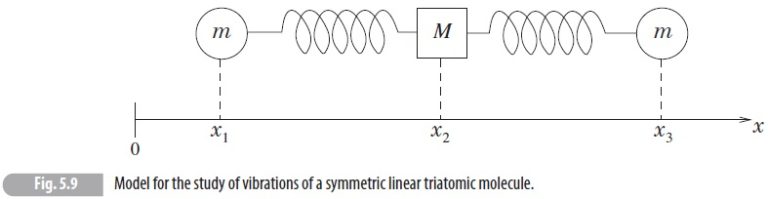
Determine the normal modes of vibration of the symmetric linear triatomic molecule (CO_{2}, for instance) represented by the model in Fig. 5.9.
Learn more on how do we answer questions.
The potential energy is given by
V= \frac{k}{2} \left(x_{2}-x_{1}-l\right)^{2}+\frac{k}{2} \left(x_{3}-x_{2}-l\right)^{2}, (5.148)
where l denotes the natural length of each spring. The equilibrium configuration is such that
0= \frac{\partial V}{\partial x_{1}}=-k\left(x_{2}-x_{1}-l\right), 0= \frac{\partial V}{\partial x_{2}}=k\left(x_{2}-x_{1}-l\right)-k\left(x_{3}-x_{2}-l\right), (5.149)
whence
x_{2}-x_{1}=l , x_{3}-x_{2}=l, (5.150)
as expected. In order to make our formalism applicable to the present problem, it is necessary to eliminate from the potential energy the terms linear in the generalised coordinates. This can be achieved by defining
\eta_{1}=x_{1}+l , \eta_{2}=x_{2} , \eta_{3}=x_{3}-l, (5.151)
leading to
L = \frac{m}{2}\left(\dot{x}^{2}_{1}+\dot{x}^{2}_{3}\right)+ \frac{M}{2}\dot{x}^{2}_{2}-V= \frac{m}{2}\left(\dot{\eta}^{2}_{1}+\dot{\eta}^{2}_{3}\right)+ \frac{M}{2}\dot{\eta}^{2}_{2}- \frac{k}{2}\left[\left(\eta_{2}-\eta_{1}\right)^{2}+\left(\eta_{3}-\eta_{2}\right)^{2}\right]. (5.152)
By inspection we identify
T=\left ( \begin{matrix} m & 0 & 0 \\ 0 & M & 0 \\ 0 & 0 & m \end{matrix} \right ) , V = \left ( \begin{matrix} k & -k & 0 \\ -k & 2k & -k \\ 0 & -k & k \end{matrix} \right ).(5.153)
The characteristic equation is written (with ω²= λ)
det(V − λT) = det \left ( \begin{matrix} k-m\lambda & -k & 0 \\ -k & 2k-M\lambda & -k \\ 0 & -k & k-m\lambda \end{matrix} \right )=0, (5.154)
whence
\left(k-m\lambda\right) \left[\left(2k-M\lambda\right)\left(k-m\lambda\right)-k^{2}\right]-k^{2}\left(k-m\lambda\right)=0. (5.155)
One immediate root is λ = k/m and the other two are the solutions of
mMλ² − k (2m + M) λ = 0 . (5.156)
Therefore, the frequencies of the normal modes are
\omega_{1}=0, \omega_{2}=\sqrt{\frac{k}{m}}, \omega_{3}=\sqrt{\frac{k}{m} \left(1+\frac{2m}{M}\right)}. (5.157)
The first characteristic frequency may look strange at first sight, inasmuch as the associated normal coordinate obeys the equation \ddot{\zeta } _{1}= 0 which does not correspond to oscillatory motion. This zero frequency mode appears because the molecule can move rigidly with unchanging potential energy. Since the restoring force against such a displacement vanishes, the associated frequency is zero. Mathematically this is due to the fact that the potential energy quadratic form is not strictly positive. Indeed, V = 0 for \eta _{1} = \eta _{2} = \eta _{3}≠ 0 and this equilibrium configuration is not stable but indifferent. The amplitude \varrho ^{(1)} associated with the frequency ω_{1} = 0 satisfies
(V-\lambda T)\varrho ^{\left(1\right) } =0 \Longrightarrow \left ( \begin{matrix} k & -k & 0 \\ -k & 2k & -k \\ 0 & -k & k \end{matrix} \right ) \left ( \begin{matrix} \varrho ^{\left(1\right) }_{1} \\ \varrho ^{\left(1\right) }_{2} \\ \varrho ^{\left(1\right) }_{3} \end{matrix} \right ) =0 \Longrightarrow \varrho ^{\left(1\right) }=A\left ( \begin{matrix} 1 \\ 1 \\ 1 \end{matrix} \right ). (5.158)
Proceeding similarly we find
\varrho ^{\left(2\right) }=B\left ( \begin{matrix} 1 \\ 0 \\ -1 \end{matrix} \right ), \varrho ^{\left(3\right) }=C \left ( \begin{matrix} 1 \\ {-2m}/{M} \\ 1 \end{matrix} \right ). (5.159)
The normal modes of vibration are sketched in Fig. 5.10. Only the modes 2 and 3 correspond to vibrations of the molecule, the mode number 1 being a rigid uniform translatory motion. The vectors \varrho ^{\left(k\right) } are associated with distinct frequencies, so they are automatically orthogonal in the inner product (5.124), as will be generally proved in the next section. The normalisation condition is
\left(\eta ,\xi \right)=\eta ^{T}T \xi \equiv \sum\limits_{kl}{T_{kl}\eta _{k}\xi _{1}}. (5.124)
\varrho ^{\left(s\right)^{T} }T \varrho ^{\left(s\right) }= \sum\limits_{kl}{T_{kl}\varrho^{\left(s\right) }_{k} \varrho^{\left(s\right) }_{l}}=1 \Rightarrow m\left(\varrho^{\left(s\right)^{2} }_{1} +\varrho^{\left(s\right)^{2} }_{3}\right)+M \varrho^{\left(s\right)^{2} }_{2} =1, s = 1, 2, 3 (5.160)
and the normalised vectors can be chosen as
\varrho^{\left(1\right)}= \frac{1}{\sqrt{2m+M} } \left ( \begin{matrix} 1 \\ 1 \\ 1 \end{matrix} \right ) , (5.161a)
\varrho^{\left(2\right)}= \frac{1}{\sqrt{2m} } \left ( \begin{matrix} 1 \\ 0 \\ -1 \end{matrix} \right ) , (5.161b)
\varrho^{\left(3\right)}= \frac{1}{\sqrt{2m \left({1+2m}/{M}\right)} } \left ( \begin{matrix} 1 \\ {-2m}/{M} \\ 1 \end{matrix} \right ) . (5.161c)
With the help of the modal matrix
A=\left ( \begin{matrix} \varrho^{\left(1\right)} & \varrho^{\left(2\right)} & \varrho^{\left(3\right)} \\ \downarrow & \downarrow & \downarrow \end{matrix} \right ), (5.162)
the normal coordinates are given by ζ = A^{T} Tη, whence, for example,
\zeta _{1}= \frac{m\eta _{1}+M\eta _{2}+m\eta _{3}}{\sqrt{2m+M} } =\frac{mx _{1}+Mx _{2}+mx _{3}}{\sqrt{2m+M}} =\left(2m+M\right)^{{1}/{2} }x _{CM}. (5.163)
There being no external forces, the centre of mass of the molecule moves with constant velocity (\ddot{x}_{CM} = 0), justifying the frequency ω_{1} = 0 associated with ζ_{1}.
