Question 9.12.6: Evaluate the line integral in Example 4....

One method of evaluating the line integral is to write

\oint_{C} =  \int_{C_{1}}+\int_{C_{2}}+\int_{C_{3}}+\int_{C_{4}}

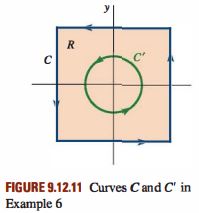
and then evaluate the four integrals on the line segments C_{1}, C_{2}, C_{3}, and C_{4}. Alternatively, if we note that the circle C^{\prime}: x^{2}+y^{2} = 1 lies entirely within C (see FIGURE 9.12.11), then from Example 5 it is apparent that P = -y /\left(x^{2}+y^{2}\right) and Q = x /\left(x^{2}+y^{2}\right) have continuous first partial derivatives in the region R bounded between C and C^{\prime}. Moreover,

\frac{\partial P}{\partial y} = \frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}} = \frac{\partial Q}{\partial x}

in R. Hence, it follows from (5) that

\oint_{C} \frac{-y}{x^{2}+y^{2}} d x+\frac{x}{x^{2}+y^{2}} d y = \oint_{C^{\prime}} \frac{-y}{x^{2}+y^{2}} d x+\frac{x}{x^{2}+y^{2}} d y .

Using the parameterization x = \cos t, y = \sin t, 0 \leq t \leq 2 \pi for C^{\prime} we obtain

\begin{aligned} \oint_{C} \frac{-y}{x^{2}+y^{2}} d x+\frac{x}{x^{2}+y^{2}} d y = & \int_{0}^{2 \pi}[-\sin t(-\sin t)+\cos t(\cos t)] d t \\ &= \int_{0}^{2 \pi}\left(\sin ^{2} t+\cos ^{2} t\right) d t & (6) \\ & =\int_{0}^{2 \pi} d t = 2 \pi . \end{aligned}