Question 20.4: Figure 20.14 shows a non-conducting rod that has a uniform p......
Figure 20.14 shows a non-conducting rod that has a uniform positive charge density +λ and a total charge Q along its right half, and a uniform negative charge density −λ and a total charge −Q along its left half. What is the direction and magnitude of the net electric field at point P that shown in Fig. 20.14?
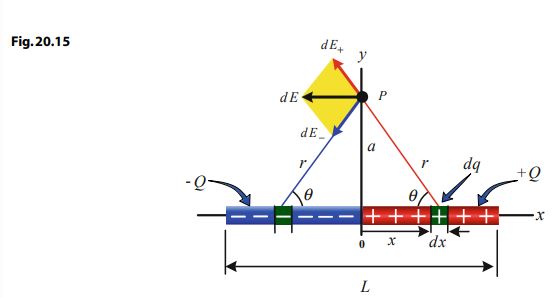
When we consider a segment dx on the right side of the rod, the charge on this segment will be dq = λ dx, see Fig. 20.15.
The electric field d\vec{E}_{+} at P due to this segment is directed outwards and away from the positive charge dq and has a magnitude:
A symmetric segment on the opposite side of the rod, but with a negative charge, creates an electric field d\vec{E}_{-} that is directed inwards and toward this segment and has the same magnitude as d \vec{E}_{+}, i.e. dE_{+} = dE_{−}. The resultant electric field d\vec{E} from both symmetric segments will be a vector to the left, see Fig. 20.15, and its magnitude will be given by:
d E=d E_{+}\cos\theta+d E_{+}\cos\theta=2\,d E_{+}\cos\theta=2\,k{\frac{\lambda\,d x}{r^{2}}}\,{\frac{x}{r}}=k\,\lambda(x^{2}+a^{2})^{-3/2}(2x)d x
The total electric field at P due to all segments of the rod is found by integrating dE from x = 0 to only x = L/2,since the negative charge of the rod is considered in evaluating dE. Thus
E=\int d E=k\lambda\int\limits_{x=0}^{x=L/2}(x^{2}+a^{2})^{-3/2}(2x\,d x)To evaluate the integral in this equation, we transform it to the form \textstyle\int u^{n}\,d u=u^{n+1}/(n+1), as we shall do in solving Eq. 20.53. Thus:
E=\int d E=\pi k\sigma a\int\limits_{0}^{R}(r^{2}+a^{2})^{-3/2}(2r\,d r) (20.53)
E=k\lambda\left|\frac{(u^{2}+a^{2})^{-1/2}}{-1/2}\right|_{u=0}^{u=L/2}=k\lambda\left[\frac{-2}{\sqrt{(L/2)^{2}+a^{2}}}-\frac{-2}{a}\right]=2k\lambda\left[\frac{1}{a}-\frac{1}{\sqrt{(L/2)^{2}+a^{2}}}\right]
When we use the fact that the magnitude of the charge Q is given by Q = λL/2, we get:
E={\frac{4k\ Q}{L}}\left[{\frac{1}{a}}-{\frac{1}{\sqrt{(L/2)^{2}+a^{2}}}}\right]When P is very far away from the rod, i.e. a >> L, we can neglect (L/2)² in the denominator of this equation and hence get E ≈ 0. In this situation, the two oppositely charged halves of the rod would appear to point P as if they were two coinciding point charges and hence have a zero net charge.
