Question 5.6: Find z-values Corresponding to Given Areas (Probabilities) (......
Find z-values Corresponding to Given Areas (Probabilities)
(a) Find k such that P(0 < z < k) = 0.3461.
(b) Find k such that P(k < z < 0) = 0.1628.
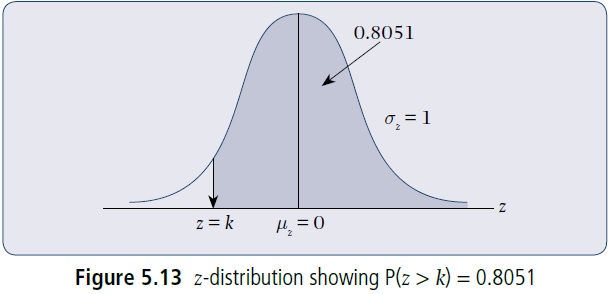
(c) Find k such that P(z > k) = 0.8051.
Learn more on how do we answer questions.
(a) This probability (area) is shown in Figure 5.11.
To find k such that P(0 < z < k) = 0.3461, the body of the z-table is scanned for the area (probability) 0.3461 (or its closest value). Then the z = k value corresponding to this area is read off.
Thus k = 1.02, since P(0 < z < 1.02) = 0.3461.
This means that 34.61% of all z-values lie between z = 0 and z = 1.02.
(b) Refer to Figure 5.12, which shows the appropriate area (probability).
From the expression (k < z < 0), k will be a negative value. Scan the z-table for an area of 0.1628. This corresponds to a z-value of 0.42. Since k is negative, k = −0.42.
Thus k = −0.42 satisfies P(−0.42 < z < 0) = 0.1628.
This means that 16.28% of all z-values lie between z = −0.42 and z = 0.
(c) Refer to Figure 5.13, which shows the appropriate area (probability).
For the area above k to be 0.8051, which is greater than 0.5, k must lie below z = 0 (the mean value of the z-distribution). Thus k will again have a negative sign.
Also, the area that must be found in the z-table is not 0.8051, but 0.3051 (i.e. 0.8051 – 0.5000), as the z-table shows areas for only half the z-distribution (i.e. between z = 0 and an upper limit z = k).
The area of 0.3051 corresponds to a z-value of 0.86.
Since k is negative, k = −0.86.
Then P(z > −0.86) = 0.8051.
This means that 80.51% of all z-values lie above z = −0.86.