Question 9.8: For the satellite of Example 9.2, which is reproduced in Fig......

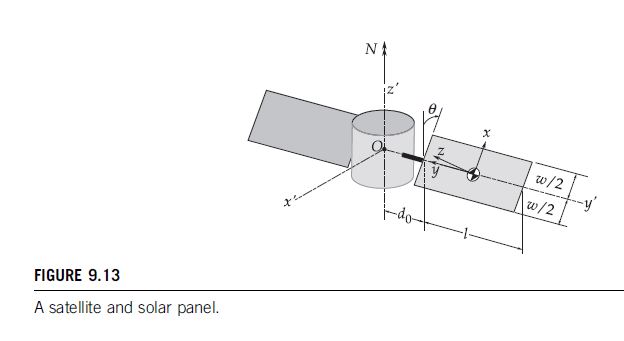
We can treat the panel as a thin parallelepiped. The panel’s xyz axes have their origin at the center of mass G of the panel and are parallel to its three edge directions. According to Figure 9.10(c), the moments of inertia relative to the xyz coordinate system are

In matrix notation,

$\left[I_G\right]=\left[\begin{array}{ccc}150.0 & 0 & 0 \\0 & 16.67 & 0 \\0 & 0 & 166.7\end{array}\right]  \left( kg \cdot m ^2\right)$                              (b)

The unit vectors of the satellite’s $x^{\prime} y^{\prime} z^{\prime}$ system are related to those of the panel’s xyz frame. By inspection,

$\begin{aligned}& \hat{ i }^{\prime}=-\sin \theta \hat{ i }+\cos \theta \hat{ k }=-0.6428 \hat{ i }+0.7660 \hat{ k } \\& \hat{ j }^{\prime}=-\hat{ j } \\& \hat{ k }^{\prime}=\cos \theta \hat{ i }+\sin \theta \hat{ k }=0.7660 \hat{ i }+0.6428 \hat{ k }\end{aligned}$                      (c)

The matrix [Q] of the transformation from xyz to $x^{\prime} y^{\prime} z^{\prime}$ comprises the direction cosines of $\hat{i}^{\prime}, \hat{j}^{\prime} \text {, and } \hat{ k }^{\prime} \text { : }$

$[ Q ]=\left[\begin{array}{ccc}-0.6428 & 0 & 0.7660 \\0 & -1 & 0 \\0.7660 & 0 & 0.6428\end{array}\right]$                           (d)

In Example 9.2, we found that the absolute angular velocity of the panel, in the satellite’s $x^{\prime} y^{\prime} z^{\prime}$ frame of reference, is

That is,

$\left\{ \omega ^{\prime}\right\}=\left\{\begin{array}{c}0 \\-0.01 \\0.1\end{array}\right\}  ( rad / s )$                    (e)

To find the absolute angular momentum $\left\{ H _G^{\prime}\right\}$ in the satellite system requires the use of Eqn (9.39),

$\left\{\begin{array}{l}H_x \\H_y \\H_z\end{array}\right\}=\left[\begin{array}{ccc}I_x & I_{x y} & I_{x z} \\I_{y x} & I_y & I_{y z} \\I_{z x} & I_{z y} & I_z\end{array}\right]\left\{\begin{array}{c}\omega_x \\\omega_y \\\omega_z\end{array}\right\}$                            (9.39a)

$\{ H \}=[ I ]\{ \omega \}$               (9.39b)

$\left\{ H _G^{\prime}\right\}=\left[ I _G^{\prime}\right]\left\{ \omega ^{\prime}\right\}$                       (f)

Before doing so, we must transform the components of the moments of the inertia tensor in Eqn (b) from the unprimed system to the primed system, by means of Eqn (9.49),

$\left[ I ^{\prime}\right]=[ Q ][ I ][ Q ]^T$                      (9.49a)

so that

$\left[I_G^{\prime}\right]=\left[\begin{array}{ccc}159.8 & 0 & 8.205 \\0 & 16.67 & 0 \\8.205 & 0 & 156.9\end{array}\right]  \left( kg \cdot m ^2\right)$                        (g)

Then Eqn (f) yields

or, in vector notation,

$H _G=0.8205 \hat{i} ^{\prime}-0.1667 \hat{ j }^{\prime}+15.69 \hat{ k }^{\prime}  \left( kg \cdot m ^2 / s \right)$                     (h)

This is the absolute angular momentum of the panel about its own center of mass G, and it is used in Eqn (9.27) to calculate the angular momentum $H _{O_{\text {rel }}}$ relative to the satellite’s center of mass O,

$H _{P_{ rel }}= H _G+ r _{G / P} \times m v _{G / P}$                       (9.27)

$H _{O_{\text {rel }}}= H _G+ r _{G / O} \times m v _{G / O}$                       (i)

$r _{G / O}$ is the position vector from O to G,

$r _{G / O}=\left(d_O+\cfrac{\ell}{2}\right) \hat{ j }^{\prime}=\left(1.5+\cfrac{6}{2}\right) \hat{ j }^{\prime}=4.5 \hat{ j }^{\prime}  ( m )$                        (j)

The velocity of G relative to O, $v _{G / O}$, is found from Eqn (9.2),

$v _B= v _A+ \omega \times R _{B / A}$                    (9.2)

$v _{G / O}= \omega _{\text {satellite }} \times r _{G / O}=N \hat{ k }^{\prime} \times r _{G / O}=0.1 \hat{ k }^{\prime} \times 4.5 \hat{ j }^{\prime}=-0.45 \hat{ i }^{\prime}   ( m / s )$          (k)

Substituting Eqns (h), (j) and (k) into Eqn (i) finally yields

Note that we were unable to use Eqn (9.21) to find the absolute angular momentum $H_O$ because that requires knowing the absolute velocity $v_G,$ which in turn depends on the absolute velocity of O, which was not provided.

$H _P= H _G+ r _{G / P} \times m v _G$                        (9.21)