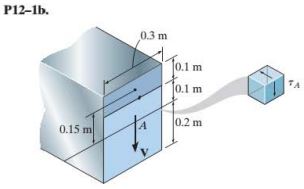
Question P12.1: In each case, calculate the value of Q and t that are used i......
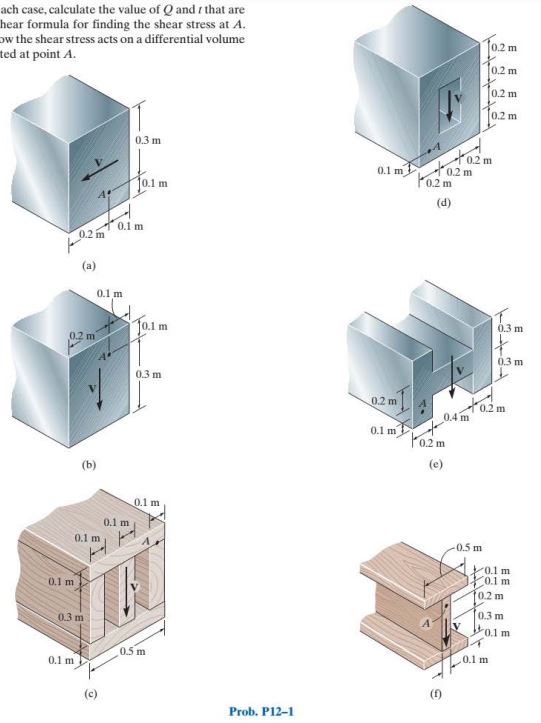
In each case, calculate the value of Q and t that are used in the shear formula for finding the shear stress at A.
Also, show how the shear stress acts on a differential volume element located at point A.
a.
\begin{aligned} Q & =\bar{y}^{\prime} A^{\prime}=(0.1 \mathrm{~m})(0.1 \mathrm{~m})(0.4 \mathrm{~m})=4\left(10^{-3}\right) \mathrm{m}^{3} \\ t & =0.4 \mathrm{~m} \end{aligned}
b.
\begin{aligned} Q & =\bar{y}^{\prime} A^{\prime}=(0.15 \mathrm{~m})(0.3 \mathrm{~m})(0.1 \mathrm{~m})=4.5\left(10^{-3}\right) \mathrm{m}^{3} \\ t & =0.3 \mathrm{~m} \end{aligned}
c.
\begin{aligned} Q & =\bar{y}^{\prime} A^{\prime}=(0.2 \mathrm{~m})(0.1 \mathrm{~m})(0.5 \mathrm{~m})=0.01 \mathrm{~m}^{3} \\ t & =3(0.1 \mathrm{~m})=0.3 \mathrm{~m} \end{aligned}
d.
\begin{aligned} Q & =\bar{y}^{\prime} A^{\prime}=(0.35 \mathrm{~m})(0.6 \mathrm{~m})(0.1 \mathrm{~m})=0.021 \mathrm{~m}^{3} \\ t & =0.6 \mathrm{~m} \end{aligned}
e.
Q=\bar{y}^{\prime} A^{\prime}=(0.25 \mathrm{~m})(0.2 \mathrm{~m})(0.1 \mathrm{~m})=5\left(10^{-3}\right) \mathrm{m}^{3} t=0.2 \mathrm{~m}
f.
\begin{aligned} Q & =\Sigma \bar{y}^{\prime} \mathrm{A}^{\prime}=(0.25 \mathrm{~m})(0.1 \mathrm{~m})(0.1 \mathrm{~m}) \\ & \quad+(0.35 \mathrm{~m})(0.1 \mathrm{~m})(0.5 \mathrm{~m})=0.02 \mathrm{~m}^{3} \end{aligned}
