Question 6.3: In the CB amplifier of Fig. 6-6(b), let hib = 30 Ω, hrb = 4 ......
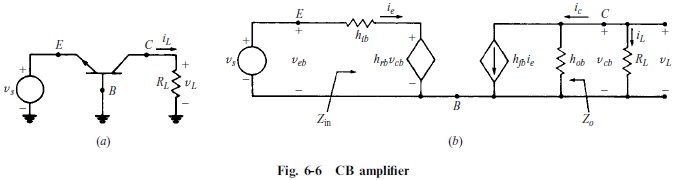
In the CB amplifier of Fig. 6-6(b), let h_{ib} = 30 Ω, h_{rb} = 4 × 10^{-6}, h_{fb} = -0.99, h_{ob} = 8 × 10^{-7} S, and R_L = 20 kΩ. (These are typical CB amplifier values.) Find expressions for the (a) current-gain ratio A_i, (b) voltage-gain ratio A_v, (c) input impedance Z_{in}, and (d) output impedance Z_o. (e) Evaluate this typical CE amplifier.
(a) By direct analogy with Fig. 6-5(b) and (6.43)
A_{i} = {\frac{i_{L}}{i_{b}}} = -{\frac{h_{fe}}{1 + h_{oe}R_{L}}} = -{\frac{100}{1 + \left(12 \times 10^{-6}\right)(2 \times 10^{3})}} = -97.7 (6.43)
A_{i} = -{\frac{h_{f b}}{1 + h_{o b}R_{L}}} = -{\frac{-0.99}{1 + (8 \times 10^{-7})(20 \times 10^{3})}} = 0.974 (6.51)
Note that A_{i} \approx -h_{fb} \lt 1, and that the input and output currents are in phase because h_{fb} < 0.
(b) By direct analogy with Fig. 6-5(b) and (6.46),
= -{\frac{(100)(2 \times 10^{3})}{1 \times 10^{3} + (2 \times 10^{3})[(1 \times 10^{3})(12 \times 10^{-6}) – (100)(1 \times 10^{-4})]}} = -199.2 (6.46)
A_{v} = -\frac{h_{f b}R_{L}}{h_{i b} + R_{L}(h_{i b}h_{o c} – h_{f b}h_{r b})} = -\frac{(-0.99)(20 \times 10^{3})}{30 + (20 \times 10^{3})[(30)(8 \times 10^{-7}) – (-0.99)(4 \times 10^{-6})]} = 647.9 (6.52)
Observe that A_{v} \approx -h_{f b}R_{L}/h_{i b}, and the output and input voltages are in phase because h_{fb} < 0.
(c) By direct analogy with Fig. 6-5(b) and (6.47)
Z_{\mathrm{in}} = {\frac{v_{s}}{i_{b}}} = h_{i e} – {\frac{h_{re}h_{f e}R_{L}}{1 + h_{oe}R_{L}}} = 1 \times 10^{3} – {\frac{(1 \times 10^{-4})(100)(2 \times 10^{3})}{1 + (12 \times 10^{-6})(2 \times 10^{3})}} = 980.5 \Omega (6.47)
Z_{\mathrm{in}} = h_{i b} – { \frac{h_{r b}h_{f b}R_{L}}{1 + h_{o b}R_{L}}} = 30 – {\frac{(4 \times 10^{-6})(-0.99)(20 \times 10^{3})}{1 + (8 \times 10^{-7})(20 \times 10^{3})}} = 30.08\,\Omega (6.53)
It is apparent that Z_{\mathrm{in}}\approx h_{ib}.
(d) By analogy with Fig. 6-5(b) and (6.50),
Z_{o} = {\frac{v_{d p}}{i_{d p}}} = {\frac{1}{h_{o e} – h_{fe}h_{r e}/h_{i e}}} = {\frac{1}{12 \times 10^{-6} – (100)(1 \times 10^{-4})/(1 \times 10^{3})}} = 500\, Ω (6.50)
Z_{o} = {\frac{1}{h_{o b} – h_{fb}h_{r b}/h_{i b}}} = {\frac{1}{8 \times 10^{-7} – (-0.99)(4 \times 10^{-6})/30}} = 1.07\,\mathrm{MQ} (6.54)
Note that Z_{o} is decreased because of the feedback from the output mesh to the input mesh through h_{rb}v_{cb}.
(e) Based on the typical values of this example, the characteristics of the CB amplifier can be summarized as follows:
1. Current gain of less than 1
2. High voltage gain
3. Power gain approximately equal to voltage gain
4. No phase shift for current or voltage
5. Small input impedance
6. Large output impedance
