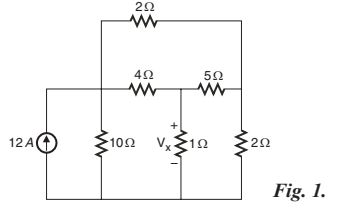
Question 2.Q.62: In the circuit of Fig. 1, calculate Vx. Prove the reciprocit......
In the circuit of Fig. 1, calculate V_x. Prove the reciprocity theorem by interchanging the positions of the 12 A source and V_x.
Learn more on how do we answer questions.
Case i : To solve V_x in the given circuit Let us assume three node voltages as shown in Fig. 2. Now the response V_x=V_2. With reference to Fig. 2, the node basis matrix equation is,
\begin{bmatrix} {{\frac{1}{4}+\frac{1}{10}}+\frac{1}{2} }&{{-\frac{1}{4}}}&-\frac{1}{4}\\ -\frac{1}{4}&{\frac{1}{4}+\frac{1}{1}}+\frac{1}{5} &-\frac{1}{5} \\ -\frac{1}{2}&-\frac{1}{5}&\frac{1}{5}+\frac{1}{2}+\frac{1}{2} \end{bmatrix} \begin{bmatrix} V _{1} \\ V _{2} \\V _{3} \end{bmatrix} =\begin{bmatrix} 12 \\ 0\\0 \end{bmatrix}
\begin{bmatrix} {0.85 }&-0.25&-0.5\\ -0.25 &1.45&-0.2\\ -0.5&-0.2&1.2 \end{bmatrix} \begin{bmatrix} V _{1} \\ V _{2} \\V _{3} \end{bmatrix} =\begin{bmatrix} 12 \\ 0\\0 \end{bmatrix} ………….(1)
\Delta ^{\prime}=\begin{vmatrix} {0.85 }&-0.25&-0.5\\ -0.25 &1.45&-0.2\\ -0.5&-0.2&1.2 \end{vmatrix} =0.85\times[(1.45\times1.2)-(-0.2)^{2}]-(-0.25)\times\left[(-0.25\times1.2)-(-0.5\times(-0.2))\right]+(-0.5)\times[(-0.25\times(-0.2))-(-0.5\times1.45)]=1.445-0.1 -0.3875=0.9575
\Delta ^{\prime}_2=\begin{vmatrix} {0.85 }&12&-0.5\\ -0.25 &0&-0.2\\ -0.5&0&1.2 \end{vmatrix} =\;0-12\times\bigl[(-0.25\times1.2)-(-0.5\times(-0.2))\bigr]+0=4.8
∴ The response,
\textstyle\mathrm{V}_{x}\,=\,\mathrm{V}_{2}\,=\,{\frac{\Delta^{\prime}_2}{\Delta^{\prime}}} ={\frac{4.8}{0.8575}}\,=\,5.0131VCase ii : To prove the reciprocity theorem by interchanging the positions of source and response
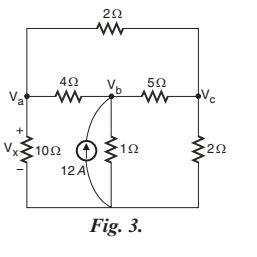
Let us interchange the positions of source and response as shown in Fig. 3. Let us assume node voltages as shown in Fig. 3. Now the response, V_x = V_a. With reference to Fig. 3, the node basis matrix equation is,
\begin{bmatrix} {{\frac{1}{4}+\frac{1}{10}}+\frac{1}{2} }&{{-\frac{1}{4}}}&-\frac{1}{2}\\ -\frac{1}{4}&{\frac{1}{4}+\frac{1}{1}}+\frac{1}{5} &-\frac{1}{5} \\ -\frac{1}{2}&-\frac{1}{5}&\frac{1}{5}+\frac{1}{2}+\frac{1}{2} \end{bmatrix} \begin{bmatrix} V _{a} \\ V _{b} \\V _{c} \end{bmatrix} =\begin{bmatrix} 0 \\ 12\\0 \end{bmatrix} ………………(2)
On comparing equations (1) and (2), we can say that the ∆^{\prime} remains the same
∴ {\Delta}^{\prime}=0.9575
\Delta ^{\prime}_a=\begin{vmatrix} {0}&-0.25&-0.5\\ 12 &1.45&-0.2\\ 0&-0.2&1.2 \end{vmatrix} =0-(-0.25)\times[12\times1.2-0]+(-0.5)\times[12\times(-0.2)-0]=3.6+1.2\;=\;4.8
∴ The response,\textstyle\mathrm{V}_{x}\,=\,\mathrm{V}_{a}\,=\,{\frac{\Delta^{\prime}_a}{\Delta^{\prime}}} ={\frac{4.8}{0.9575}}\,=\,5.0131V
Here, the response {V}_{x} remains the same after interchanging the positions of source and response. Hence, the reciprocity theorem is proved.