Question 3.27: In the RLC circuit of Fig. 1, the inductor has an initial cu......
In the RLC circuit of Fig. 1, the inductor has an initial current of 10 A, when the switch is closed at t = 0. Find an expression for the current i (t).
Let, \mathcal{L}\{i(t)\}=I(\mathbf{s})
Also,\mathcal{L}\{200\} =\frac{200}{s}
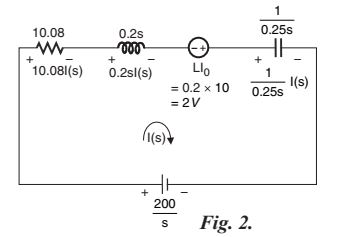
The s-domain equivalent of the given RLC circuit is shown in Fig. 2.With reference to Fig. 2, we can write
10.08 I(s)+0.2 s I(s)+\frac{1}{0.25 s} I(s)=\frac{200}{s}+2\\ I ( s )\left[10.08+0.2 s +\frac{1}{0.25 s }\right]=\frac{200+2 s }{ s }\\ \therefore I ( s )=\frac{200+2 s }{ s } \times \frac{1}{10.08+0.2 s +\frac{1}{0.25 s }} =\frac{200+2 s }{10.08 s +0.2 s ^2+\frac{1}{0.25}}=\frac{200+2 s }{0.2\left( s ^2+\frac{10.08}{0.2} s +\frac{1}{0.2 \times 0.25}\right)}=\frac{1000+10 s }{ s ^2+50.4 s +20}The roots of quadratic, s² + 50 .4s + 20 = 0 are,
s=\frac{-50.4 \pm \sqrt{50.4^2-4 \times 20}}{2} \\ =\frac{-50.4 \pm 49.6}{2}=-0.4,-50 \\ \therefore I(s) =\frac{1000+10 s}{(s+0.4)(s+50)}I ( s )=\frac{1000+10 s }{( s +0.4)( s +50)}=\frac{ K _1}{ s +0.4}+\frac{ K _2}{ s +50} \\ K _1=\frac{1000+10 s }{( s +0.4)( s +50)} \times\left.( s +0.4)\right|_{ s =-0.4} \\ \quad=\left.\frac{1000+10 s }{ s +50}\right|_{ s =-0.4}=\frac{1000+10 \times(-0.4)}{-0.4+50}=20.0806 \approx 20 \\ K _2=\frac{1000+10 s }{( s +0.4)( s +50)} \times\left.( s +50)\right|_{ s =-50} \\ \quad=\left.\frac{1000+10 s }{ s +0.4}\right|_{ s =-50}=\frac{1000+10 \times(-50)}{-50+0.4}=-10.0806 \approx-10 \\ \therefore I( s )=\frac{20}{ s +0.4}-\frac{10}{ s +50}
Let us take the inverse Laplace transform of I (s).
\mathcal{L}^{-1}\{ I ( s )\} = L ^{-1}\left\{\frac{20}{ s +0.4}-\frac{10}{ s +50}\right\} \\ \therefore i( t ) =20 e ^{-0.4 t }-10 e ^{-50 t } A \\ =10\left(\frac{20}{10} e ^{-0.4 t }- e ^{-50 t }\right) A \\ =10\left(2 e ^{-0.4 t }- e ^{-50 t }\right) A\mathcal{L} \left\{ e ^{- at }\right\}=\frac{1}{ s + a }
