Question 17.1: Induction-Motor Performance A certain 30-hp four-pole 440-V-......
Induction-Motor Performance
A certain 30-hp four-pole 440-V-rms 60-Hz three-phase delta-connected induction motor has
R_s = 1.2 Ω R_r^{'} = 0.6 Ω
X_s = 2.0 Ω X_r^{'} = 0.8 Ω
X_m = 50 Ω
Under load,the machine operates at 1746 rpm and has rotational losses of 900W. Find the power factor, the line current, the output power, copper losses, output torque, and efficiency.
Learn more on how do we answer questions.
From Table 17.1, we find that synchronous speed for a four-pole motor is n_s = 1800 rpm. Then, we utilize Equation 17.16 to compute the slip:
s = \frac{\omega_s – \omega_m}{\omega_s} = \frac{n_s – n_m}{n_s} (17.16)
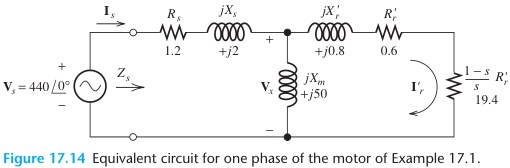
s = \frac{n_s – n_m}{n_s} = \frac{1800-1746}{1800}=0.03We can use the data given to draw the equivalent circuit shown in Figure 17.14 for one phase of the motor. The impedance seen by the source is
Z_s = 1.2 + j2+ \frac{j50(0.6 +19.4 +j0.8)}{j50+0.6+19.4+j0.8}
=1.2+j2 +16.77+j7.392
=17.97 + j9.392
=20.28 \angle 27.59° \Omega
The power factor is the cosine of the impedance angle. Because the impedance is inductive, we know that the power factor is lagging:
power factor = cos(27.59°) = 88.63% lagging
For a delta-connected machine, the phase voltage is equal to the line voltage, which is specified to be 440 V rms. The phase current is
I_s = \frac{V_s}{Z_s} = \frac{440 \angle 0°}{20.28 \angle 27.59°}=21.70 \angle -27.59° A rms
Thus, the magnitude of the line current is
I_{line} = I_s \sqrt{3} = 21.70 \sqrt{3} = 37.59 A rms
The input power is
P_{in} = 3I_sV_s \cos θ
= 3(21.70)440 \cos(27.59°)
= 25.38 kW
Next, we compute V_x and I_r^{'}:
V_x = I_s \frac{j50 (0.6+19,4+j0.8)}{j50 +0.6+19,4+j0.8}
= 21.70 ∠−27.59° × 18.33 ∠23.78°
= 397.8 ∠−3.807° V rms
I_r^{'} = \frac{V_x}{j0.8 + 0.6 + 19.4}
=\frac{397.8 \angle -3.807°}{20.01 \angle 1.718°}
= 19.88 \angle -5.52° A rms
The copper losses in the stator and rotor are
P_s = 3R_sI_s^2
= 3(1.2)(21.70)^2
= 1695 W
and
P_r = 3R_r^{'}(I_r^{'})^2
= 3(0.6)(19.88)^2
= 711.4 W
Finally, the developed power is
P_{dev} = 3 \times \frac{1-s}{s}R_r^{'}(I_r^{'})^2
=3(19.4)(19.88)^2
=23.00 kW
As a check, we note that
P_{in} = P_{dev} + P_s + P_r
to within rounding error.
The output power is the developed power minus the rotational loss, given by
P_{out} = P_{dev} − P_{rot}
= 23.00 − 0.900
= 22.1 kW
This corresponds to 29.62 hp, so the motor is operating at nearly its rated load. The output torque is
T_{out} = \frac{P_{out}}{\omega _m}
=\frac{22,100}{1746(2 \pi / 60)}
=120.9 Nm
The efficiency is
\eta = \frac{P_{out}}{P_{in}}\times 100\%
=\frac{22,100}{25,380} \times 100 \%
= 87.0 \%
Table 17.1. Synchronous Speed versus Number of Poles for f = 60 Hz
| P | n_s |
| 2 | 3600 |
| 4 | 1800 |
| 6 | 1200 |
| 8 | 900 |
| 10 | 720 |
| 12 | 600 |