Question 12.114: KNOWN: Flat plate exposed to night sky and in ambient air at......
KNOWN: Flat plate exposed to night sky and in ambient air at \mathrm T_{\text{air}} = 15°C with a relative humidity of 70%. Radiation from the atmosphere or sky estimated as a fraction of the blackbody radiation corresponding to the near-ground air temperature, \mathrm G_{\text{sky}} = ε_{\text{sky}} σ \mathrm T_{\text{air}}, and for a clear night, ε_{\text{sky}} = 0.741 + 0.0062 \mathrm T_{\mathrm{dp}} \text {where} \mathrm T_{\mathrm{dp}} is the dew point temperature (°C). Convection coefficient estimated by correlation, \overline{\mathrm h}\left(W / m ^2 \cdot K \right)=1.25 \Delta\mathrm T ^{1 / 3} where ∆T is the plate-to-air temperature difference (K).
FIND: Whether dew will form on the plate if the surface is (a) clean metal with ε_{\mathrm m} = 0.23 and (b) painted with ε_{\mathrm p} = 0.85.
ASSUMPTIONS: (1) Steady-state conditions, (2) Surfaces are diffuse, gray, and (3) Backside of plate is well insulated.
PROPERTIES: Psychrometric charts (Air), \mathrm T_{\mathrm{dp}} = 9.4°C for dry bulb temperature 15°C and relative humidity 70%.
SCHEMATIC:
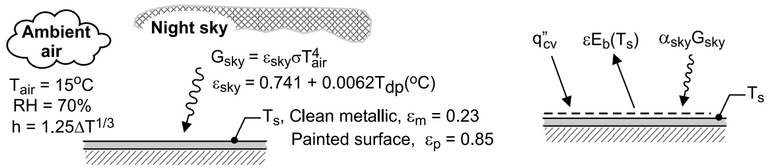
Learn more on how do we answer questions.
ANALYSIS: From the schematic above, the energy balance on the plate is
\dot{ E }_{\text {in}}^{\prime \prime}-\dot{ E }_{\text {out}}^{\prime \prime}=0
\alpha_{\text {sky}} G _{\text {sky}}+ q _{\text{cv}}^{\prime \prime}-\varepsilon E _{ b }\left( T _{ s }\right)=0
\varepsilon\left[\left\lgroup 0.741+0.0062 T _{ dp }\left({ }^{\circ} C \right)\right\rgroup \sigma T _{\text {air}}^4\right]+1.25\left( T _{\text {air}}- T _{ s }\right)^{4 / 3} W / m ^2-\varepsilon \sigma T _{ s }^4 W / m ^2=0
where G _{\text {sky}}=\varepsilon_{\text {sky}} \sigma T _{\text{air}}, \varepsilon_{\text {sky}}=0.741+0.062 T _{ dp }\left({ }^{\circ} C \right) ; T _{ dp } has units (°C); and, other temperatures in kelvins. Since the surface is diffuse-gray, \alpha_{\text {sky}}=\varepsilon.
(a) Clean metallic surface, ε_m = 0.23
0.23\left[\left\lgroup 0.741+0.0062 T _{ dp }\left({ }^{\circ} C \right)\right\rgroup \sigma(15+273)^4 K ^4\right] +1.25\left(289- T _{ s , m }\right)^{4 / 3} W / m ^2-0.23 \sigma T _{ s , m }^4 W / m ^2=0
T _{ s , m }=282.7 K =9.7^{\circ}C
(b) Painted surface, ε_p = 0.85 T_{s,p} = 278.5 K = 5.5^{\circ}C
COMMENTS: For the painted surface, ε_{\mathrm p} = 0.85, find that \mathrm T_{\mathrm s} < \mathrm T_{\mathrm{dp}}, so we expect dew formation. For the clean, metallic surface, \mathrm T_{\mathrm s} > \mathrm T_{\mathrm{dp}}, so we do not expect dew formation.