Question 12.116: KNOWN: Plate temperature and spectral absorptivity of coatin......
KNOWN: Plate temperature and spectral absorptivity of coating.
FIND: (a) Solar irradiation, (b) Effect of solar irradiation on plate temperature, total absorptivity, and total emissivity.
ASSUMPTIONS: (1) Steady-state, (2) Opaque, diffuse surface, (3) Isothermal plate, (4) Negligible radiation from surroundings.
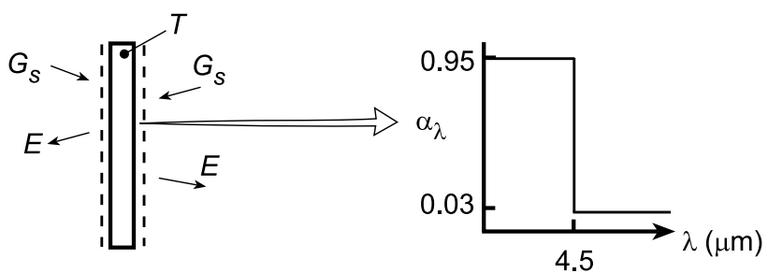
SCHEMATIC:
ANALYSIS: (a) Performing an energy balance on the plate, 2α_SG_S – 2E = 0 and
\alpha_{ S } G _{ S }-\varepsilon \sigma T ^4=0
For λT = 4.5 µm × 2000 K = 9000 µm⋅K, Table 12.1 yields F_{(o→λ)} = 0.890. Hence,
\varepsilon=\varepsilon_1 F _{(0 \rightarrow \lambda)}+\varepsilon_2\left(1- F _{( o \rightarrow \lambda)}\right)=0.95 \times 0.890+0.03(1-0.890)=0.849
For λT = 4.5 µm × 5800 K = 26,100, F_{(o→λ)} = 0.993. Hence,
\alpha_{ S }=\alpha_1 F_{(0 \rightarrow \lambda)} +\alpha_2\left(1- F _{(0 \rightarrow \lambda)}\right)=0.95 \times 0.993+0.03 \times 0.007=0.944
Hence,
G _{ S }=\left(\varepsilon / \alpha_{ S }\right) \sigma T ^4=(0.849 / 0.944) 5.67 \times 10^{-8} W / m ^2 \cdot K ^4(2000 K )^4=8.16 \times 10^5 W / m ^2
(b) Using the IHT First Law Model and the Radiation Toolpad, the following results were obtained.
The required solar irradiation increases with T to the fourth power. Since α_S is determined by the spectral distribution of solar radiation, its value is fixed. However, with increasing T, the spectral distribution of emission is shifted to lower wavelengths, thereby increasing the value of ε.
