Question 4.19: Lifetimes of batteries in a certain application are normally......
Lifetimes of batteries in a certain application are normally distributed with mean 50 hours and standard deviation 5 hours. Find the probability that a randomly chosen battery lasts between 42 and 52 hours.
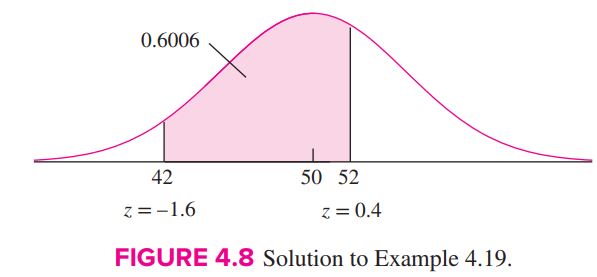
Let X represent the lifetime of a randomly chosen battery. Then X ∼ N(50, 5^{2}). Figure 4.8 presents the probability density function of the N(50, 5^{2}) population. The shaded area represents P(42 < X < 52), the probability that a randomly chosen battery has a lifetime between 42 and 52 hours. To compute the area, we will use the z table. First we need to convert the quantities 42 and 52 to standard units. We have
z = \frac{42\ −\ 50}{5} = −1.60 z =\frac{ 52\ −\ 50}{5} = 0.40
From the z table, the area to the left of z = −1.60 is 0.0548, and the area to the left of z = 0.40 is 0.6554. The probability that a battery has a lifetime between 42 and 52 hours is 0.6554 − 0.0548 = 0.6006.
