Question 39.53: Schrödinger’s equation for states of the hydrogen atom for w......
Schrödinger’s equation for states of the hydrogen atom for which the orbital quantum number \ell is zero is
\frac{1}{r^2} \frac{d}{d r}\left(r^2 \frac{d \psi}{d r}\right)+\frac{8 \pi^2 m}{h^2}[E-U(r)] \psi=0 .
Verify that Eq. 39-39, which describes the ground state of the hydrogen atom, is a solution of this equation.
\psi(r)=\frac{1}{\sqrt{\pi} a^{3 / 2}} e^{-r / a} \quad \text { (ground state) } (39-39)
THINK The ground state of the hydrogen atom corresponds to n = 1, \ell= 0, and m_\ell = 0.
EXPRESS The proposed wave function is
\psi=\frac{1}{\sqrt{\pi} a^{3 / 2}} e^{-r / a}
where a is the Bohr radius. Substituting this into the right side of Schrödinger’s equation, our goal is to show that the result is zero.
ANALYZE The derivative is
\frac{d \psi}{d r}=-\frac{1}{\sqrt{\pi} a^{5 / 2}} e^{-r / a}
so
r^2 \frac{d \psi}{d r}=-\frac{r^2}{\sqrt{\pi} a^{5 / 2}} e^{-r / a}
and
\frac{1}{r^2} \frac{d}{d r}\left( r^2 \frac{d \psi}{d r}\right)=\frac{1}{\sqrt{\pi} a^{5 / 2}}\left(-\frac{2}{r}+\frac{1}{a}\right)e^{-r / a}=\frac{1}{a}\left( -\frac{2}{r}+\frac{1}{a}\right) \psi \text {. }
The energy of the ground state is given by E=-m e^4 / 8 \varepsilon_0^2 h^2 and the Bohr radius is given by a=h^2 \varepsilon_0 / \pi m e^2 , so E=-e^2 / 8 \pi \varepsilon_0 a . The potential energy is given by
U=-e^2 / 4 \pi \varepsilon_0 r,
so
\begin{aligned} \frac{8 \pi^2 m}{h^2} E-U \psi & =\frac{8 \pi^2 m}{h^2} \left(\,-\frac{e^2}{8 \pi \varepsilon_0 a}+\frac{e^2}{4 \pi \varepsilon_0 r}\right) \psi=\frac{8 \pi^2 m}{h^2} \frac{e^2}{8 \pi \varepsilon_0} \left(-\frac{1}{a}+\frac{2}{r}\right) \psi \\ & =\frac{\pi m e^2}{h^2 \varepsilon_0} \left(\,-\frac{1}{a}+\frac{2}{r}\right) \psi=\frac{1}{a} \left(-\frac{1}{a}+\frac{2}{r} \right) \psi . \end{aligned}
The two terms in Schrödinger’s equation cancel, and the proposed function \psi satisfies that equation.
LEARN The radial probability density of the ground state of hydrogen atom is given by Eq. 39-44:
P(r)=\frac{4}{a^3} r^2 e^{-2 r / a} (radial probability density, hydrogen atom ground state). (39-44)
P(r)=|\psi|^2\left(4 \pi r^2\right)=\frac{1}{\pi a^3} e^{-2 r / a}\left(4 \pi r^2\right)=\frac{4}{a^3} r^2 e^{-2 r / a} .
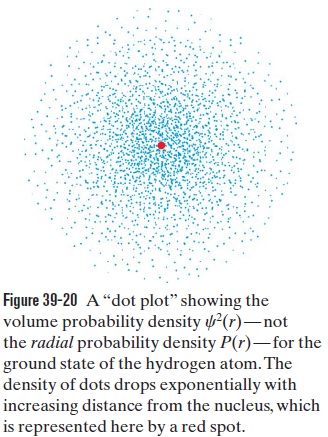
A plot of P(r) is shown in Fig. 39-20.
