Question 3.WP.18: The following is a highly simplified mechanism for the decom......
The following is a highly simplified mechanism for the decomposition of C3H8:
\mathrm{C}_{3}\mathrm{H}_{8}\;{\xrightarrow{k_{1}}}\mathrm{C}\mathrm{H}_{3}^{•}+\mathrm{C}_{2}\mathrm{H}_{5}^{•}
\mathrm{CH}_{3}^{•}+\mathrm{C}_{3}\mathrm{H}_{8}\stackrel{k_{2}}{\longrightarrow}\mathrm{CH}_{4}+\mathrm{C}_{3}\mathrm{H}_{7}^{•}
{\mathsf{C}}_{3}{\mathsf{H}}_{7}^{•}{\xrightarrow{k_{3}}}\,{\mathsf{C}}_{2}{\mathsf{H}}_{4}+{\mathsf{C}}{\mathsf{H}}_{3}^{•}
\mathrm{CH}_{3}^{•}+\mathrm{CH}_{3}^{•}\stackrel{k_{4}}{\longrightarrow}\mathrm{C}_{2}\mathrm{H}_{6}
Pick out the intermediates and formulate a steady state expression, +d[intermediate]/dt ≈0, where possible. From these, find expressions for each steady state concentration, and then formulate the overall rate of reaction in terms of the rate of production of {\mathrm{CH}}_{4}.
- Intermediates are \mathrm{CH}_{3}^{•},\,\mathrm{C}_{2}\mathrm{H}_{5}^{•}\mathrm{~and~}\mathrm{C}_{3}\mathrm{H}_{7}^{•}.
- {\mathrm{CH}}_{3}^{•} is formed in steps 1 and 3 and removed in steps 2 and 4
- \mathrm{C}_{2}\mathrm{H}_{5}^{•} is formed in step 1, but the step or steps removing \mathrm{C}_{2}\mathrm{H}_{5}^{•} are not given and so a steady state equation cannot be written
- C_{3}\mathrm{H}_{7}^{•} is formed in step 2 and removed in step 3.
- Steady state equations: these are always written in terms of production of the intermediate i.e. +ve for rates of production and -ve for rates of removal.
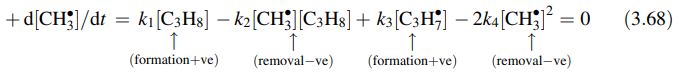
The factor of two arises because the steady state equation is written in terms of the rate of production of {\mathrm{CH}}_{3}^{•}, and for every step 4, two {\mathrm{CH}}_{3}^{•}, are removed.
Both these equations are equations in two unknowns, and neither can be solved on its own. They are simultaneous equations, solved by adding (3.68) + (3.69).
- k_{1}[\mathbf{C}_{3}\mathbf{H}_{8}]=2k_{4}[\mathbf{C}\mathbf{H}_{3}^{•}]^{2} ∴ [{\bf C H}_{3}^{•}]=(k_{1}/2k_{4})^{1/2}[{\bf C}_{3}{\bf H}_{8}]^{1/2} (3.70)
- Substituting into (3.69) gives [{\bf C}_{3}{H}_{7}^{•}]=\frac{k_{2}}{k_{4}}\left(\frac{k_{1}}{2k_{4}}\right)^{1/2}[{\bf C}_{3}{\bf H}_{8}]^{3/2} (3.71)
- Rate of reaction = k_{2}[{\bf C H}_{3}^{•}][{\bf C}_{3}{\bf H}_{8}]=k_{2}(k_{1}/2k_{4})^{1/2}[{\bf C}_{3}{\bf H}_{8}]^{3/2} (3.72)