Question 10.SP.2: The uniform column AB consists of an 8-ft section of structu......
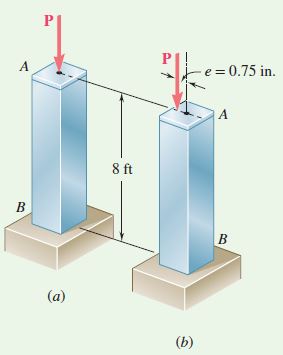
The uniform column AB consists of an 8-ft section of structural tubing with the cross section shown. (a) Using Euler’s formula and a factor of safety of 2, determine the allowable centric load for the column and the corresponding normal stress. (b) Assuming that the allowable load found in part a is applied at a point 0.75 in. from the geometric axis of the column, determine the horizontal deflection of the top of the column and the maximum normal stress in the column. Use E=29 \times 10^6 psi.
STRATEGY: For part a, use the factor of safety with Euler’s formula to determine the allowable centric load. For part b, use Eqs. (10.31) and (10.35) to find the horizontal deflection and maximum normal stress in the column, respectively.
y_{\max }=e\left(\sec \frac{\pi}{2} \sqrt{\frac{P}{P_{ cr }}}-1\right) (10.31)
\sigma_{\max }=\frac{P}{A}\left(1+\frac{e c}{r^2} \sec \frac{\pi}{2} \sqrt{\frac{P}{P_{ cr }}}\right) (10.35)

Learn more on how do we answer questions.
MODELING:
Effective Length. Since the column has one end fixed and one end free, its effective length is
L_e=2(8 \text{ft})=16 \text{ft} =192 \text { in. }
Critical Load. Using Euler’s formula,
P_{ cr }=\frac{\pi^2 E I}{L_e^2}=\frac{\pi^2\left(29 \times 10^6 psi \right)\left(8.00 in ^4\right)}{(192 in .)^2} \quad P_{ cr }=62.1 kips
ANALYSIS:
a. Allowable Load and Stress. For a factor of safety of 2,
P_{\text {all }}=\frac{P_{ cr }}{F . S .}=\frac{62.1 kips }{2} \quad P_{\text {all }}=31.1 kips
and
\sigma=\frac{P_{\text {all }}}{A}=\frac{31.1 kips }{3.54 in ^2} \quad \sigma=8.79 ksi
b. Eccentric Load (Fig. 1). Observe that column AB and its load are identical to the upper half of the column of Fig. 10.20, which was used for the secant formulas. Thus, the formulas of Sec. 10.2 apply directly here.
Recalling that P_{ all } / P_{ cr }=\frac{1}{2} and using Eq. (10.31), the horizontal deflection of point A is
\begin{aligned} y_m & =e\left[\sec \left(\frac{\pi}{2} \sqrt{\frac{P}{P_{ cr }}}\right)-1\right]=(0.75 \text { in. })\left[\sec \left(\frac{\pi}{2 \sqrt{2}}\right)-1\right] \\ & =(0.75 \text { in. })(2.252-1) \end{aligned}
y_m=0.939 in .
This result is illustrated in Fig. 2.
The maximum normal stress is obtained from Eq. (10.35) as
\begin{aligned} & \sigma_m=\frac{P}{A}\left[1+\frac{e c}{r^2} \sec \left(\frac{\pi}{2} \sqrt{\frac{P}{P_{\text {cr }}}}\right)\right] \\ & =\frac{31.1 kips }{3.54 in ^2}\left[1+\frac{(0.75 in .)(2 in .)}{(1.50 in .)^2} \sec \left(\frac{\pi}{2 \sqrt{2}}\right)\right] \\ & =(8.79 ksi )[1+0.667(2.252)] \end{aligned}
\sigma_m=22.0 ksi


