Question 11.2.4: A 150-ft foot bridge crossing a gorge is suspended from two ...
UNIFORMLY LOADED CABLE WITH SUPPORTS AT UNEQUAL HEIGHTS
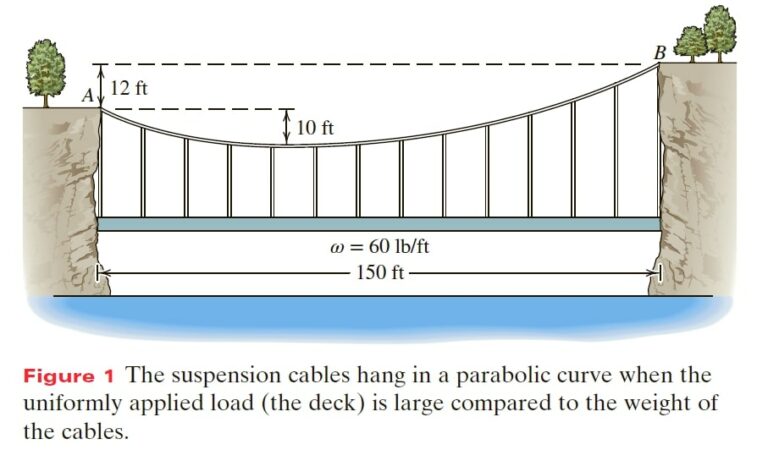
A 150-ft foot bridge crossing a gorge is suspended from two cables. Due to the natural terrain, the right support is 12 ft higher than the left support. The weight of the bridge deck and handrails supported by the cables is 60 lb/ft (Figure 1) and the lowest point of the cables is 10 ft below the left support. Determine the maximum and minimum cable tensions, the angle between the cables and the horizontal at the right support, and the total length of each cable.
Learn more on how we answer questions.
Goal For each cable find the maximum and minimum cable tensions, the angle between the cable and the horizontal at B, and the total length.
Given Information about the cable geometry and loading.
Assume The cable is inextensible and the cable weight is negligible relative to the loading.
Draw We define a coordinate system with its origin at the lowest point of the cable, the location of which is unknown (Figure 2). We define x_{B} as the x coordinate of support B; then the coordinate x_{A}= x_{B}− 150 ft .
Formulate Equations and Solve The load is shared equally by the two suspension cables; therefore ω = 30 lb/ft for each cable. We locate the origin by applying (11.3A) at supports A and B:
y=\frac{\omega x^{2}}{2T_{O}} (11.3A)
At A : y_{A}=10 ft = \frac{\left(30 lb/ft\right) \left(x_{B} – 150 ft\right)^{2} }{2T_{O}} (1)
At B : y_{B}=22 ft = \frac{\left(30 lb/ft\right) \left(x_{B} \right)^{2} }{2T_{O}} (2)
We eliminate T_{O} by dividing (1) by (2), which gives
\frac{10 ft}{22 ft} = \frac{\left(x_{B} – 150 ft\right)^{2}}{x^{2}_{B}}
Rearranging and simplifying produces an equation that can be solved using the quadratic formula:
x^{2}_{B} – 550 x_{B} + 41, 250 =0
x_{B} =\frac{550\pm \sqrt{\left(- 550\right)^{2}- 4(1)(41, 250)} }{2(1)} =275 ft \pm 185.4 ft \Rightarrow x_{B} =460.4 ft or 89.6 ft
We discard x_{B}= 460.4 ft because it is not a realistic solution when the constraints of this problem are considered. Therefore x_{B}= 89.6 ft . Substituting this value of x_{B} into (2), we solve for the minimum cable tension T_{O}
y_{B}=\frac{\omega x^{2}_{B}}{2T_{O}} =22 ft = \frac{\left(30 lb/ft\right)\left(89.6 ft\right)^{2} }{2T_{O}} \Rightarrow T_{O}=5475 lb
T_{max} occurs at support B, because the slope of the cable is steepest there.
Using (11.4), we find T_{max} :
T^{2}=\omega ^{2} x^{2} +T_{O}^{2} or T =\sqrt{\omega ^{2} x^{2} + T_{O}^{2}} (11.4)
T_{max} =T_{@ x=89.6 ft}=\sqrt{\left\lgroup30\frac{lb}{ft} \right\rgroup^{2} \left(89.6 ft\right)^{2} + \left(5474 lb\right)^{2} } \Rightarrow T_{max} =6098 lb
The tensile force is tangent to the cable at any point along the cable. Therefore, the angle the cable force makes with the horizontal and the angle the cable makes with the horizontal are the same. We call this angle \theta _{B} at support B. Figure 3 shows the relationship between the cable force at B and the horizontal component of that force.
T_{Bx}=T_{B}\cos \theta _{B} \Rightarrow \theta _{B} =\cos ^{-1} \left\lgroup\frac{5474 lb}{6098 lb} \right\rgroup \Rightarrow \theta _{B} =26.2^{\circ }
Finally, to find the length of the cable L, substitute x_{A}= 89.6 ft−150 ft = −60.4 ft , x_{B}= 89.6 ft , T_{O}= 5474 lb , and ω = 30 lb/ft into (IV.5A):
L = – s_{OA} + s_{OB}=- \left[x_{A}+ \frac{\omega ^{2} x^{3}_{A}}{ 6T_{O}^{2}} – \frac{\omega ^{4} x^{5}_{A}}{ 40T_{O}^{4}}\right] + \left[x_{B}+ \frac{\omega ^{2} x^{3}_{B}}{ 6T_{O}^{2}} – \frac{\omega ^{4} x^{5}_{B}}{ 40T_{O}^{4}}\right]
L=154.6 ft
Check Aside from rechecking calculations, there are no alternative calculations that serve as a check for this problem.

