Question 15.18: A 16 ft wide irrigation channel is equipped with a sharp-edg...
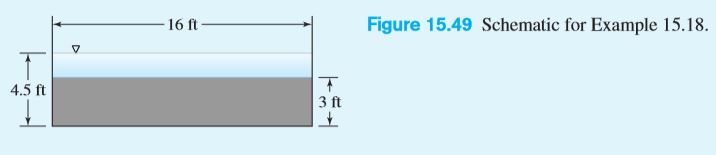
A 16 ft wide irrigation channel is equipped with a sharp-edged, full-width rectangular weir as shown in Figure 15.49. The weir height is 3 ft, and at the maximum design flow the upstream water depth is 4.5 ft. What is the discharge under these conditions? What is the discharge of a 90° V-notch weir with the same weir head?
Learn more on how we answer questions.
We can calculate the flowrate of a full-width rectangular weir by using Eqs. 15.62a and 15.62b, noting that the weir head y1 − yW = 4.5 ft − 3.0 ft = 1.5 ft exceeds the minimum required value of 0.2 ft. To calculate the discharge coefficient we use Eq. 15.62b: CW = 0.59 + 0.08[(y1 − yW)/yw]. Inserting the data, we have CW = 0.59 + 0.08[(4.5 − 3)/3] = 0.63. The flowrate is then found by using Eq. 15.62a:
Q=C_Ww\left(\frac{L}{w} \right)\sqrt{g}(y_1-y_W)^{3/2}
=0.63(16\ \mathrm{ft})\left(\frac{16\ \mathrm{ft}}{16\ \mathrm{ft}} \right)\sqrt{32.2\ \mathrm{ft}/s^2}(4.5\ \mathrm{ft}-3\ \mathrm{ft})^{3/2}=105\ \mathrm{ft}^3/s
The 90° V-notch weir is described by Eqs. 15.63. Combining these equations and noting that θ = 90°, we have
Q=C_W(\tan \frac{\theta }{2})\sqrt{g}(y_1-y_W)^{5/2} (15.63a)
C_W=0.44 (15.63b)
Q = 0.44\sqrt{g} (y1 − yW)5/2 = 0.44\sqrt{32.2\ \mathrm{ft}/s^2}(4.5 ft − 3 ft )5/2 = 6.9 ft3/s