Question 12.S-P.8: A 5-m-long, simply supported steel beam AD is to carry the d...
A 5-m-long, simply supported steel beam AD is to carry the distributed and concentrated loads shown. Knowing that the allowable normal stress for the grade of steel to be used is 160 MPa, select the wide-flange shape that should be used.
Reactions. Considering the entire beam as a free body, we write
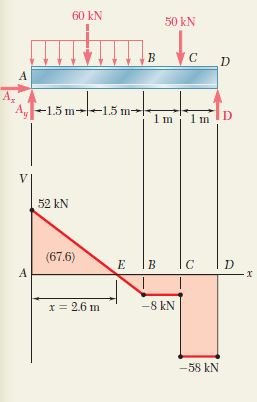
+\curvearrowleft \sum{M_{A}} = 0: D(5 m) – (60 kN) (1.5 m) – (50 kN) (4 m) = 0D = 58.0 kN D = 58.0 kN↑
\underrightarrow{+} \sum{F_{x}} = 0: A_{x} = 0+↑ \sum{F_{y}} = 0: A_{y} + 58.0 kN – 60 kN – 50 kN = 0
A_{y} = 52.0 kN A = 52.0 kN↑
Shear Diagram. The shear just to the right of A is V_{A} = A_{y} = + 52.0 kN. Since the change in shear between A and B is equal to minus the area under the load curve between these two points, we have
V_{B} = 52.0 kN – 60 kN = 28 kN
The shear remains constant between B and C, where it drops to -58 kN, and keeps this value between C and D. We locate the section E of the beam where V = 0 by writing
V_{E} – V_{A} = -wx
0 – 52.0 kN = -(20 kN/m) x
Solving for x, we find x = 2.60 m.
Determination of |M|_{max}. The bending moment is maximum at E, where V = 0. Since M is zero at the support A, its maximum value at E is equal to the area under the shear curve between A and E. We have, therefore, |M|_{max} = M_{E} = 67.6 kN \cdot m.
Minimum Allowable Section Modulus. Substituting into Eq. (12.9) the givenn value of σ_{all} and the value of |M|_{max} that we have found, we write
S_{min} = \frac{|M|_{max}}{σ_{all}} =\frac{67.6 kN \cdot m}{160 MPa} = 422.5 × 10^{-6} m^{3} = 422.5 × 10^{3} mm^{3}
Selection of Wide-Flange Shape. From App. B we compile a list of shapes that have a section modulus larger than S_{min} and are also the lightest shape in a given depth group.
| S, mm^{3} | Shape |
| 629 | W410 × 38.8 |
| 475 | W360 × 32.9 |
| 547 | W310 × 38.7 |
| 531 | W250 × 44.8 |
| 451 | W200 × 46.1 |
We select the lightest shape available, namely W360 × 32.9
