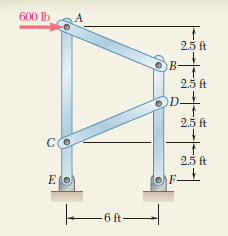
Question 6.S-P.6: A 600-lb horizontal force is applied to pin A of the frame s...
Vector Mechanics for Engineers: Statics and Dynamics [987614]
Statics and Mechanics of Materials
Vector Mechanics for Engineers Statics and Dynamics [1686025]
Vector Mechanics for Engineers Statics and Dynamics [1694543]
Statics and Mechanics of Materials
A 600-lb horizontal force is applied to pin A of the frame shown. Determine the forces acting on the two vertical members of the frame.
Learn more on how we answer questions.
Free Body: Entire Frame. The entire frame is chosen as a free body; although the reactions involve four unknowns, E_{y} and F_{y} may be determined by writing
+\curvearrowleft \sum{M_{E}} = 0: -(600 lb)(10 ft) + F_{y}(6 ft) = 0F_{y} = +1000 lb F_{y} = 1000 lb↑
+↑ \sum{F_{y}} = 0: E_{y} + F_{y} = 0E_{y} = -1000 lb E_{y} = 1000 lb↓
Members. The equations of equilibrium of the entire frame are not sufficient to determine E_{x} and F_{x}. The free-body diagrams of the various members must now be considered in order to proceed with the solution. In dismembering the frame, we will assume that pin A is attached to the multiforce member ACE and, thus, that the 600-lb force is applied to that member. We also note that AB and CD are two-force members.
Free Body: Member ACE
+↑ \sum{F_{y}} = 0: -\frac{5}{13}F_{AB} + \frac{5}{13}F_{CD} – 1000 lb = 0+\curvearrowleft \sum{M_{E}} = 0: -(600 lb)(10 ft) – (\frac{12}{13}F_{AB})(10 ft) – (\frac{12}{13}F_{CD})(2.5 ft) = 0
Solving these equations simultaneously, we find
F_{AB} = -1040 lb F_{CD} = +1560 lb
The signs obtained indicate that the sense assumed for F_{CD} was correct and the sense for F_{AB} incorrect. Summing now x components,
\underrightarrow{+} \sum{F_{x}} = 0: 600 lb + \frac{12}{13}(-1040 lb) + \frac{12}{13}(+1560 lb) + E_{x} = 0E_{x} = -1080 lb E_{x} = 1080 lb←
Free Body: Entire Frame. Since E_{x} has been determined, we can return to the free-body diagram of the entire frame and write
\underrightarrow{+} \sum{F_{x}} = 0: 600 lb – 1080 lb + F_{x} = 0F_{x} = +480 lb F_{x} = 480 lb→
Free Body: Member BDF (Check). We can check our computations by verifying that the equation \sum{M_{B}} = 0 is satisfied by the forces acting on member BDF.
+\curvearrowleft \sum{M_{B}} = -(\frac{12}{13}F_{CD})(2.5 ft) + (F_{x})(7.5 ft)
=-\frac{12}{13}(1560 lb)(2.5 ft) + (480 lb)(7.5 ft)
= -3600 lb \cdot ft + 3600 lb \cdot ft = 0 (checks)
