Holooly Plus Logo
Holooly Plus Logo

Question 4.3: A collection of 60 laser diodes were tested, and 7 failures ...

A collection of 60 laser diodes were tested, and 7 failures occurred after 1000 h. The lifetimes obtained are tabulated below.

Rank number (i) Lifetime (h) F(t_{i})=(i-0.3)/(60+0.4)
1 181 0.012              (1.2%)
2 299 0.028             (2.8%)
3 389 0.045             (4.5%)
4 430 0.061              (6.1%)
5 535 0.078             (7.8%)
6 610 0.094             (9.4%)
7 805 0.111                (11.1%)

1. Plot the results in both Weibull and lognormal fashion.
2. What is the MTTF for each?
3. For the lognormal plot, what is the value of σ?
4. For the Weibull plot, what is α?

The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
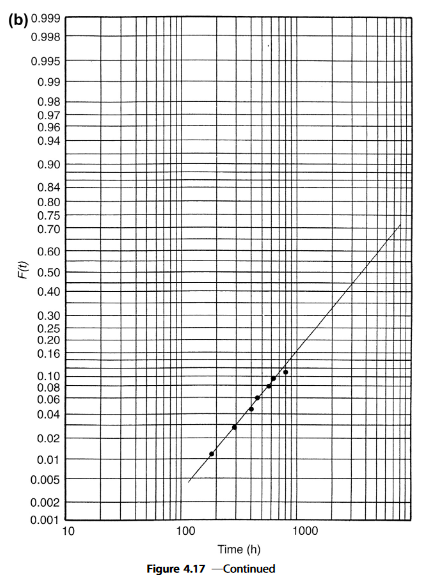
  1. First, F(t_{i}) is calculated for n = 60 and i = 1, 2, 3,…, 7 and entered in the table.
    The F values are plotted versus log time on Weibull and lognormal paper as shown in Figure 4.17(a) and (b).
  2. At a value of F = 0.5, MTTF = 2170 h (Weibull) and 3600 h (lognormal).
  3. It was shown above that \sigma=\ln[t_{0.5}/t_{0.159}]. Substituting, \sigma =\ln[3600/980]=1.30.
  4. From Eqn (4.16) \ln[1-F(t)]=-(t/ \alpha)^{\beta} we note that when t = α ,\ln[1-F(t)]=-1.Thus,1-F(t)=0.368, and F(t)=0.632. At this value, which is noted on the ordinate axis, α = t = 2990 h.
4.17 a
4.17 b

Related Answered Questions

Question: 4.4

Consider a 50-pin module such that the probability of failure upon inserting it into a mating connector is 1.8 × 10^-3 % per pin. What is the probability of failure of the module? ...

Verified Answer:

In this problem the module is the system (s), and ...
Question: 4.1

Suppose that a population of 525,477 solid-state devices is burned in at elevated temperature, and the number of failed devices are weeded out as a function of time is recorded in the following table. Determine the failure rates, λ(t), at the indicated times. ...

Verified Answer:

Results of the calculations are tabulated. Tim...
Question: 4.6

Suppose that ICs are used in a critical application at 40°C. The manufacturer selects a sample population of 1000 chips, ages them at 150°C for 2 years (ta = 1.75 × 10^4 h) and no failures are observed. Typical data for other similar products suggest that the activation energy for failure is 0.4 eV ...

Verified Answer:

First the AF is evaluated from Eqn (4.36): ...
Question: 4.2

Suppose the population of devices is described by the life distribution F(t) = 1 – exp(-0.0001t). 1. What is the probability that a new device will fail after 1000 h? After 5000 h? Between these times? 2. What is the failure rate at 1000 h? After 5000 h? ...

Verified Answer:

By substitution, F(t)=1-exp[-0.0001(1000)]=...
Question: 4.5

Tantalum capacitors were tested at elevated temperature, and the failure times were Weibull distributed with scale parameter α = 2.5 × 10^5 h and a shape parameter β = 0.5. If the AF is estimated to be 1 × 10^4 , what is the probability that the capacitors will last 1 year? ...

Verified Answer:

The failure probability is given by F(t)=1-...