Question 8.9: A CONTINUATION OF EXAMPLE 5.5, WITH THE ADDITION SHOWN IN IT...
A CONTINUATION OF EXAMPLE 5.5, WITH THE ADDITION SHOWN IN ITALIC TYPE
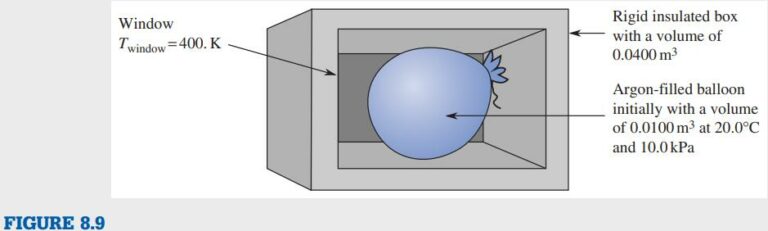
A new radiation heat transfer sensor consists of a small, closed, rigid, insulated 0.0400 \text{m³} box containing a 0.0100 \text{m³} rubber balloon. Initially, the box is evacuated but the balloon contains argon (an ideal gas) at 20.0°\text{C } and 0.0100 \text{MPa} . When the balloon receives 0.100 \text{kJ } of radiation energy through an uninsulated window in the box, it bursts. The resulting pressure change is sensed by a pressure transducer and an alarm is sounded. Determine the pressure and temperature inside the box after the balloon bursts and the entropy produced during this process if the average surface temperature of the heat transfer window is 400. \text{K}
Learn more on how we answer questions.
First, draw a sketch of the system (Figure 8.9).
The unknown is the entropy produced during this process if the average surface temperature of the heat transfer window is 400. \text{K}. The material is argon gas.
In Example 5.5, we use an energy balance to find the final pressure and temperature as p_2 = 4.15 \text{kPa } and T_2 = 214° \text{C }= 487 \text{K}. Now, an entropy balance gives
\frac{_1Q_2}{T_b} + _1(S_P)_2 = m(s_2 − s_1)_\text{argon}
which can be solved for the entropy production as
_1(S_P)_2 = m(s_2 − s_1) – \frac{_1Q_2}{T_b}
and, since argon is an ideal gas, we can write
s_2 − s_1 = c_p \text{ln} (T_2/T_1) – R \text{ln} (p_2/p_1)
From Table C.13b of Thermodynamic Tables to accompany Modern Engineering Thermodynamics, we find that for argon, c_p = 0.523 \text{ kJ/kg .K} and R = 0.208 \text{ kJ/kg .K} ; and from Example 5.5, the mass of the argon is m = 0.00164 \text{kg}. Then, with _1Q_2 = 0.100 \text{kJ } and T_b = 400. \text{ K}, we get
_1(S_P)_2 = (0.00164 \text{kg})[( 0.523 \text{ kJ/kg .K})\text{ln}(\frac{214 + 273.15 \text{K}}{20.0 + 273.15 \text{K}} ) – (0.208 \text{ kJ/kg .K})\text{ln}(\frac{4.15 \text{kPa}}{10.0 \text{kPa}}) ]
-\frac{0.100 \text{kJ}}{400. \text{ K}} = 0.486 × 10^{-3} \text{ kJ/k} = 0.486 \text{ J/K}
In this example, the heat transfer occurs over only a portion of the system’s surface (the uninsulated window). The rest of the enclosure is insulated to prevent the sensor from being influenced by anything except the heat source in front of the window. Though the surface temperature of the window probably changes during the heat transfer process, an adequate solution is obtained simply by using an average surface temperature during the process of T_b = 400. \text{K} .