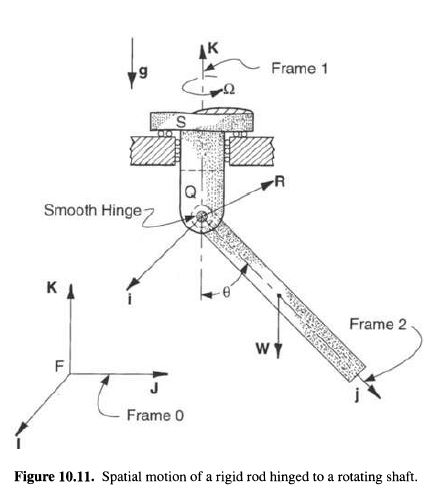
A homogeneous thin rod of mass m and length l is connected to a vertical shaft S by a smooth hinge bearing at Q. The shaft rotates with a constant angular velocity Ω, as shown in Fig. 10.11. (i) Derive the equation of motion of the rod. (ii) Determine as a function of θ the hinge bearing reaction

Question

A homogeneous thin rod of mass m and length [latex]\mathcal{l}[/latex] is connected to a vertical shaft S by a smooth hinge bearing at [latex]\mathcal{Q}[/latex]. The shaft rotates with a constant angular velocity Ω, as shown in Fig. 10.11. (i) Derive the equation of motion of the rod. (ii) Determine as a function of θ the hinge bearing reaction torque exerted on the rod at [latex]\mathcal{Q}[/latex], for the initial data [latex]\dot{ heta}(0)=0 ext { at } heta(0)= heta_0 [/latex]. (iii) Analyze the infinitesimal stability of the relative equilibrium states of the rod.

Accepted Answer

(i). The central point [latex]\mathcal{Q}[/latex] at the hinge being fixed in the inertial (machine) frame [latex]0=\left\{F ; \mathbf{I} _k ight\}[/latex], the equation of motion for the rod is obtained from Euler's law (10.66) in the principal body frame [latex]2 = \left\{\mathcal{Q ; \mathbf{i}_{k}} ight\} [/latex]. We need [latex]\mathbf{ω} , \mathbf{I}_{\mathcal{Q}}, ext{ and } \mathbf{M}_{\mathcal{Q}}[/latex].

[latex]M_1^Q=I_{11}^Q \dot{\omega}_1+\omega_2 \omega_3\left(I_{33}^Q-I_{22}^Q ight)[/latex],

[latex]M_2^Q=I_{22}^Q \dot{\omega}_2+\omega_3 \omega_1\left(I_{11}^Q-I_{33}^Q ight),[/latex] (10.66)

[latex]M_3^Q=I_{33}^Q \dot{\omega}_3+\omega_1 \omega_2\left(I_{22}^Q-I_{11}^Q ight)[/latex].

Let [latex]\mathbf{k} = \mathbf{i} _3[/latex] denote the hinge axis at [latex]\mathcal{Q}[/latex]. Then the total angular velocity [latex]\omega ≡ \omega_{20}[/latex] of the rod (frame 2) relative to the machine (frame 0) is the sum of the angular velocity [latex]\omega _{21}=\dot{ heta} \mathbf{k}[/latex] of the rod relative to the vertical shaft (frame 1 ) and the angular velocity [latex]\omega _{10}= \Omega =\pmb{\Omega} \mathbf{K}[/latex] of the shaft relative to the machine. Thus, referred to the rod frame 2,

[latex]\omega =-\Omega(\sin heta \mathbf{i} +\cos heta \mathbf{j} )+\dot{ heta} \mathbf{k}[/latex], (10.80a)

and hence the total angular acceleration of the rod is

[latex]\dot{\omega}=-\Omega \dot{ heta}(\cos heta \mathbf{i} -\sin heta \mathbf{j} )+\ddot{ heta} \mathbf{k}.[/latex] (10.80b)

The rod frame at [latex]\mathcal{Q}[/latex] is a principal body frame relative to which

[latex]\mathbf{I} _Q=\frac{1}{3} m \ell^2\left( \mathbf{i} _{11}+ \mathbf{i} _{33} ight)[/latex] (10.80c)

in accordance with (9.46d), with a change of axes in mind. Finally, the moment of the forces and torques acting on the rod about Q is

[latex]\mathbf{I} _H\left( \mathcal{B} _r ight)=\frac{m \ell^2}{3}\left( \mathbf{i}_{11}+ \mathbf{i}_{22} ight)[/latex] (9.46d)

[latex]\mathbf{M} _\mathcal{Q}=\mu_1 \mathbf{i} +\mu_2 \mathbf{j} - m g \frac{\ell}{2} \sin heta \mathbf{k} .[/latex] (10.80d)

Here [latex]\mu_1 ext { and } \mu_2[/latex] are unknown components of the torque exerted on the rod by the smooth hinge bearing for which [latex]\mu_3=0[/latex], and the weight W of the homogeneous rod acts at its center of mass at [latex]\mathbf{x} ^*=\ell / 2 \mathbf{j}[/latex] .

Use of (10.80a) through (10.80d) in Euler's equations (10.66) yields the components of the smooth hinge bearing reaction torque exerted on the rod at Q,

[latex]\mu_1=-\frac{2}{3} m \ell^2 \Omega \dot{ heta} \cos heta, \quad \mu_2=\mu_3=0[/latex] (10.80e)

and the different ial equation of motion of the rod,

[latex]\ddot{ heta}+\left(p^2-\Omega^2 \cos heta ight) \sin heta=0, \quad p^2 \equiv \frac{3 g}{2 \ell} .[/latex] (10.80f)

With the aid of this result, the reader may now determine from Euler' s first law the resultant hinge reaction force R at Q.

When Ω = 0, [latex]\mu_{1} = 0[/latex] and ( 10.80f) reduces to the familiar pendulum equation.
In this case, the circular frequency p for the rod is the same as that of a simple pendulum of length L = 2l/3. Therefore, the exact and approximate solutions for the vibration of the rod when Ω = 0 may be read from those for the simple pendulum. We next consider the case when Ω ≠ 0.

(ii).

To determine the hinge bearing reaction torque (10.80e) as a function of θ, we need [latex] \dot{ heta}( heta)[/latex], the first integral of (10.80f). With [latex]\ddot{ heta}=d\left(\frac{1}{2} \dot{ heta}^2 ight) / d heta[/latex],

separation of the variables and use of the initial data [latex]\dot{ heta}(0) = 0 ext{ at } heta(0) = heta_{0}[/latex] yields

[latex]\dot{ heta}= \pm \sqrt{\Omega^2\left(\cos ^2 heta_0-\cos ^2 heta ight)+3 \frac{g}{\ell}\left(\cos heta-\cos heta_0 ight)}[/latex] (10.80g)

Substitution of this result into (10.80e) delivers as a function of 0 the hinge bearing
reaction torque exerted on the rod at Q:

[latex]\mu_1=\mp \frac{2}{3} m \ell^2 \Omega \cos heta \sqrt{\Omega^2\left(\cos ^2 heta_0-\cos ^2 heta ight)+3 \frac{g}{\ell}\left(\cos heta-\cos heta_0 ight)}[/latex]. (10.80h)

Notice that the reaction torque [latex]\mu_{1}( heta)[/latex] vanishes when [latex] heta= heta_0[/latex] or nπ/2 (n odd) and, of course, also when Ω =o.

(iii). The relative equilibrium states [latex] heta_{s}[/latex] of the rod, by (10.80f), are given by

[latex]\left(p^2-\Omega^2 \cos heta_s ight) \sin heta_s=0[/latex], (10.80i)

which yields three distinct states

[latex] heta_s=0, \pi, \quad heta_s=\cos ^{-1}\left(\frac{p^2}{\Omega^2} ight) .[/latex] (10.80j)

To examine the infinitesimal stability of these states , introduce [latex] heta = heta_{s} + δ[/latex], where δ is an infinitesimal angular disturbance from [latex] heta_{s}[/latex] Then recalling (10.80i) and retaining only terms of the first order in δ, we obtain from (10.80f),

[latex]\ddot{\delta}+\left\{\left[p^2-\Omega^2 \cos heta_s ight] \cos heta_s+\Omega^2 \sin ^2 heta_s ight\} \delta=0[/latex]. (10.80k)

Therefore, the disturbance is bounded and simple harmonic, and hence infinitesimally stable, if and only if the coefficient

[latex]\omega^2 \equiv\left[p^2-\Omega^2 \cos heta_s ight] \cos heta_s+\Omega^2 \sin ^2 heta_s>0 .[/latex] (10.80l)

We now recall (10.80j). First consider [latex] heta_{s} = 0[/latex] Then (10.80l) requires [latex]\omega^{2} = p^2-\Omega^2>0[/latex]. Hence, the relative equilibrium state [latex] heta_{s} = 0[/latex] is infinitesimally stable if and only if [latex]\Omega

[latex]\Omega_c \equiv p=\sqrt{\frac{3 g}{2 \ell}}[/latex], (10.80m)

which is independent of the mass of the rod. In this case, the small amplitude circular frequency of the rod oscillations about the vertical state [latex] heta_s=0[/latex] is [latex] \omega_v \equiv \left(p^2-\Omega^2 ight)^{1 / 2} ext {. }[/latex]

Of course, the inverted vertical configuration of the rod [latex] heta_{s} = \pi[/latex] is impractic al in respect of the suggested design in Fig. 10.11. Even so, (10.80l) fails for [latex] heta_{s} = \pi[/latex] , and hence the inverted relative equilibrium state of the rod is inherently unstable for all angular speeds of the vertical shaft.

Notice that when [latex]\Omega=\Omega_c=p, \omega^2 \leq 0[/latex] for all positions (10.80j ). Hence, no infinitesimally stable relative equilibrium states of the rod exist at the critical angular speed [latex]\Omega=\Omega_c[/latex].

Finally, consider the case [latex]\cos heta_s=p^2 / \Omega^2[/latex] This requires p/ Ω < l ; hence (10.80l) is satisfied, and the relative equilibrium state [latex] heta_{s} = cos^{- 1}(p^2/ \Omega^2)[/latex], regardless of the mass of the rod, is infinitesimally stable if and only if [latex]\Omega>p=\Omega_c[/latex]. The small amplitude vibrational frequency of the rod about this displaced relative equilibrium state is [latex]\omega_d \equiv \Omega\left(1-p^4 / \Omega^4 ight)^{1 / 2}[/latex].

In sum, if [latex]\Omega<\Omega_c[/latex], the vertical relative equilibrium position of the rod is its only infinitesimally stable relative equilibrium state. When the vertical shaft attains its critical angular speed, [latex]\Omega =\Omega_c[/latex] , however, no infinitesimally stable relative equilibrium positions of the rod exist. Afterwards, when [latex]\Omega >\Omega_c[/latex], the displaced configuration of the rod at [latex] heta_s=\cos ^{-1}\left(p^2 / \Omega^2 ight)[/latex] is its only infinitesimally stable relative equilibrium position.

Question 10.10: A homogeneous thin rod of mass m and length l is connected t...

Related Answered Questions

Verified Answer:

Use the results for Example 10.3, page 424, to determine (i) the total torque about the hinge Q, and (ii) the total torque about the center of mass C, required to sustain the motion of the thin rod. ...

Verified Answer:

(i) Apply (10.95) to determine the total kinetic energy of the connecting rod of the simple machine shown in Fig. 10.6, page 425. (ii) Repeat the calculation based on (10.94). ...

Verified Answer:

Apply the energy principle to derive the first integral of the equation of motion for the physical pendulum in Fig. 10.15, page 467 . ...

Verified Answer:

Apply the energy method to derive the first integral of the equation of motion of the rod described in Fig. 10.11, page 447. ...

Verified Answer:

Verified Answer:

Verified Answer:

Verified Answer:

Gravitational potential energy. Determine the total gravitational potential energy of a body B in a uniform gravitational field of strength g per unit mass a of B. ...

Verified Answer:

Apply the foregoing results to find the moment of momentum relative to Q for the connecting rod of the simple machine in Fig. 10.6, page 425. ...

Verified Answer: