Question 6.12: A load admittance has the value yL = 0.2 − j0.5 . Find the l...
A load admittance has the value yL = 0.2 − j0.5 . Find the locations where a matching admittance should be placed. In addition, find the value for the matching admittance.
Learn more on how we answer questions.
The input admittance will have the value yin = 1 ± jb at two locations that can be obtained from the Smith chart by rotating the load admittance on a constant reflection:coefficient circle. This value has already been determined from the value at the load admittance. At these locations, the real part and the imaginary part of the reflection coefficient will be
\mathcal{R} _{r}=\frac{ b ^{2}}{4+ b ^{2}} \quad \mathcal{R} _{i}=\frac{2 b }{4+ b ^{2}}
where we have inserted g=1 in (6.42) and have understood the Smith chart in terms of the admittance. Since the magnitude of the reflection coefficient is already known ( |\mathcal{R}|=0.7257) , we just have to solve the algebraic equation for the value of the susceptance b that must be inserted at these locationands
\mathcal{R} = \mathcal{R} _{r}+ j \mathcal{R} _{i}=\frac{ Z _{ L }-1}{ Z _{ L }+1} (6.42)
|\mathcal{R} |^{2}=\left(\frac{b^{2}}{4+b^{2}}\right)^{2}+\left(\frac{2 b}{4+b^{2}}\right)^{2}
This equation results in the following algebraic equation that must be solved.
\left(1-|\mathcal{R} |^{2}) b^{4}+\left(4-8|\mathcal{R} |^{2}\right) b^{2}-16|\mathcal{R} |^{2}=0\right.
The roots of this polynomial are calculated to be
b^{2}=4.45 ; b^{2}=-4
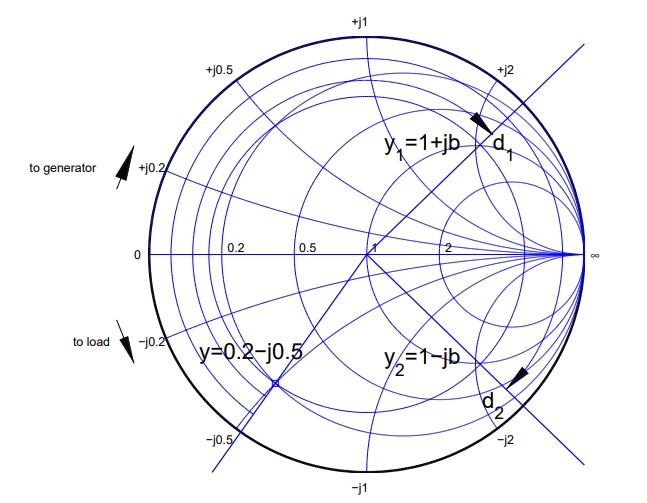
and because b must be a real number we neglect the second solution. Thus, we find two real solutions b_{1} \approx 2.11 and b_{2} \approx -2.11, which are in good agreement with the two graphical solutions, obtained from the Smith chart. The above calculation using the Smith chart is shown below.
The location of the load admittance is indicated with a and the radius of the circle which passes through this point is equal to the magnitude of the reflection coefficient circle. The circle passes through the “g = 1” circle at two locations. The closest one is at a distance d1 from the load admittance. One should insert an admittance equal to –jb at that location. The transmission line will be matched from that point back to the signal generator. There is a second location d2 that is further from the load admittance where one could insert an admittance that is equal to +jb and could be used if it is inconvenient to choose the first location.