Question 11.5: A pipeline conveys 8.33 litre per second of water from an ov...
A pipeline conveys 8.33 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03.)
The height H of the overhead tank above the building can be determined from the conditions with a single pipe.
H=h_{f}=0.03 \frac{2000}{0.15}\left[\frac{(4 \times 0.00833)}{\pi(0.15)^{2}}\right]^{2} \frac{1}{2 \times 9.81}=4.53 m
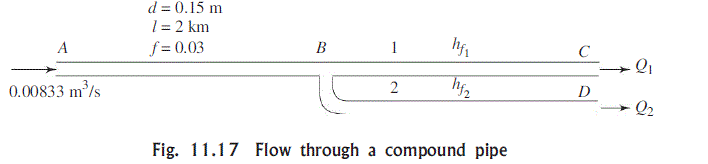
In the new plan as shown in Fig. 11.17
h_{f}=4.53=h_{f_{A B}}+h_{f_{B C}} (11.39)
again,
h_{f_{B C}}=h_{f_{B D}}=\frac{f L_{1}}{2 g d_{1}}\left[\frac{4 Q_{1}}{\pi\left(d_{1}\right)^{2}}\right]^{2}=\frac{f L_{2}}{2 g d_{2}}\left[\frac{4 Q_{2}}{\pi\left(d_{2}\right)^{2}}\right]^{2}
Here, L_{1}=L_{2}=1000 m
Therefore, \left(Q_{1} / Q_{2}\right)^{2}=\left(d_{1} / d_{2}\right)^{5} (11.40)
h_{f_{A B}}=\frac{0.03 \times 1000}{2 g(0.15)}\left[\frac{4 Q}{\pi(0.15)^{2}}\right]^{2}
Therefore, Eq. (11.39) can be written as
\frac{0.03 \times 1000 \times 8 Q^{2}}{9.81 \times \pi^{2} \times(0.15)^{5}}+\frac{0.03 \times 1000 \times 8 \times Q_{1}^{2}}{9.81 \times \pi^{2} \times(0.15)^{5}}=4.53 (11.41)
In this case, Q=1.3 \times 0.00833=0.0108 m ^{3} / s
Then, from Eq. (11.41), we get
Q_{1}^{2}=0.00014-(0.0108)^{2}
which gives Q_{1}=0.0048 m ^{3} / s
From continuity, Q_{2}=0.0108-0.0048=0.006 m ^{3} / s
From Eq. (11.40), we have d_{2}=\left(\frac{0.006}{0.0048}\right)^{2 / 5} \times 0.15
= 0.164 m
It can be observed from Eq. (11.41) that
Q_{1}^{2}=0.00014-Q^{2}
or Q^{2}=0.00014-Q_{1}^{2}
Now Q will be maximum when & \dot{Q}_{1} will be minimum. For a physically possible situation, the minimum value of & \dot{Q}_{1} will be zero. Therefore, the maximum value of Q will be
Q_{\max }=\sqrt{0.00014}=0.0118 m ^{3} / s
which is 41.6% more than the initial value. The case \left(Q_{1}=0, Q=0.0118 m ^{3} / s \right) corresponds to a situation of an infinitely large branched pipe, i.e. d_{2} \rightarrow \infty \text {. }
