Question 11.4: A pipeline of 0.6 m in diameter is 1.5 km long. In order to ...
A pipeline of 0.6 m in diameter is 1.5 km long. In order to augment the discharge, another parallel line of the same diameter is introduced in the second half of the length. Neglecting minor losses, find the increase in discharge if f = 0.04. The head at inlet is 30 m over that at the outlet.
Initially, for the single pipe, the discharge is calculated from the relationship
\Delta H=h_{f}=f \frac{L}{D} \frac{V^{2}}{2 g}
The average flow velocity V=\frac{4 Q}{\pi D^{2}}
Hence, \Delta H=\frac{16}{\pi^{2} \times 2 \times g} \frac{f L}{D^{5}} Q^{2}
(where ΔH is the difference in head between the inlet and outlet at the pipe and h_{f} is the frictional head loss).
or Q^{2}=\frac{30 \times \pi^{2} \times 2 \times 9.81 \times(0.6)^{5}}{16 \times 0.04 \times 1500}
or Q = 0.686 m ^{3} / s
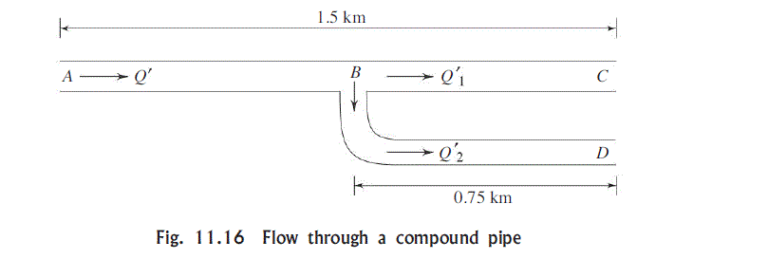
Let Q^{\prime} be the discharge through the first half of the pipe when another parallel line of same diameter is introduced to the second half of the length as shown in Fig. 11.16. If Q_{1}^{\prime} and Q_{2}^{\prime} are the flow rates through the two branched pipes in parallel, then from continuity,
Q^{\prime}=Q_{1}^{\prime}+Q_{2}^{\prime}
We can write for the two parallel paths BC and BD
H_{B}-H_{C}=\frac{0.04 \times 0.75}{0.6 \times 2 \times 9.81}\left[\frac{4}{\pi(0.6)^{2}}\right]^{2} Q_{1}^{\prime 2}
H_{B}-H_{D}=\frac{0.04 \times 0.75}{0.6 \times 2 \times 9.81}\left[\frac{4}{\pi(0.6)^{2}}\right]^{2} Q_{2}^{2}
At outlet, H_{C}=H_{D}
Therefore, we get from the above two equations along with the equation of continuity
Q_{1}^{\prime}=Q_{2}^{\prime}=Q^{\prime} / 2
Applying Bernoulli’s equation between A and C through the hydraulic path ABC, we have
30=\frac{0.04 \times 0.75 \times 10^{3}}{0.6 \times 2 \times 9.81}\left[\frac{4}{\pi(0.6)^{2}}\right]^{2} Q^{\prime 2}
+\frac{0.04 \times 0.75 \times 10^{3}}{0.6 \times 2 \times 9.81}\left[\frac{4}{\pi(0.6)^{2}}\right]^{2}\left(\frac{Q^{\prime}}{2}\right)^{2}
=39.85 Q^{\prime 2}
which gives Q^{\prime} = 0.868 m^{3} / s
Therefore, the increase in the rate of discharge by the new arrangement becomes
Q^{\prime}-Q=0.868-0.686=0.182 m^{3} / s
which is 0.182 × 100/0.686 = 26.4% of the initial rate of discharge.
