Question 23.8: A Plane of Charge Find the electric field due to an infinite...
A Plane of Charge
Find the electric field due to an infinite plane of positive charge with uniform surface charge density σ.
Learn more on how we answer questions.
Conceptualize Notice that the plane of charge is infinitely large. Therefore, the electric field should be the same at all points equidistant from the plane. How would you expect the electric field to depend on the distance from the plane?
Categorize Because the charge is distributed uniformly on the plane, the charge distribution is symmetric; hence, we can use Gauss’s law to find the electric field.
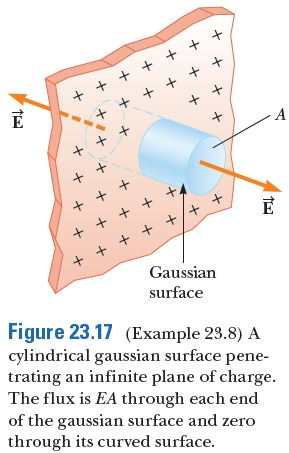
Analyze By symmetry, \overrightarrow{E} must be perpendicular to the plane at all points. The direction of \overrightarrow{E} is away from positive charges, indicating that the direction of \overrightarrow{E} on one side of the plane must be opposite its direction on the other side as shown in Figure 23.17. A gaussian surface that reflects the symmetry is a small cylinder whose axis is perpendicular to the plane and whose ends each have an area A and are equidistant from the plane. Because \overrightarrow{E} is parallel to the curved surface of the cylinder—and therefore perpendicular to d \overrightarrow{A} at all points on this surface—condition (3) is satisfied and there is no contribution to the surface integral from this surface. For the flat ends of the cylinder, conditions (1) and (2) are satisfied. The flux through each end of the cylinder is EA; hence, the total flux through the entire gaussian surface is just that through the ends, \Phi_E=2 E A.
Write Gauss’s law for this surface, noting that the enclosed charge is q_{\text {in }}=\sigma A :
\Phi_E=2 E A=\frac{q_{\text {in }}}{\epsilon_0}=\frac{\sigma A}{\epsilon_0}Solve for E:
E=\frac{\sigma}{2 \epsilon_0} (23.9)
Finalize Because the distance from each flat end of the cylinder to the plane does not appear in Equation 23.9, we conclude that E=\sigma / 2 \epsilon_0 at any distance from the plane. That is, the field is uniform everywhere. Notice that this is the same result as that obtained in Example 23.3, where we let the radius of a disk of charge become infinite. Figure 23.18 shows this uniform field due to an infinite plane of charge, seen edge-on.