Question 11.1: A scattering medium between diffuse-gray walls is nonabsorbi...
A scattering medium between diffuse-gray walls is nonabsorbing, κ = 0, σ_s > 0, and conducts heat with a constant thermal conductivity k. The wall temperatures are T_1 and T_2, and the spacing between the walls is D. Determine the energy transfer from wall 1 to wall 2.
For pure scattering the temperature distribution within the layer does not enter into the radiative solution as given by Equations 11.64 and 11.65,
\frac{q_r}{\sigma (T_1^4-T_2^4)}=\frac{\psi _b}{1+\psi _b(1/\epsilon _1+1/\epsilon _2-2)} (11.64)
\frac{Γ(\tau )/\sigma -T_2^4}{T_1^4-T_2^4}=\frac{\phi _b(\tau )+[(1-\epsilon _2)/\epsilon _2]\psi _b}{1+\psi _b(1/\epsilon _1+1/\epsilon _2-2)} (11.65)
and ∇ ⋅ q_r = 0 as shown by Equation 10.40. Hence, in the absence of absorption, the energy equation that determines the heat conduction is independent of the scattering process. The energy transfer is then found by adding to Equation 11.64 the heat conduction as if scattering were not present,
q=\frac{k(T_1-T_2)}{D}+\frac{\sigma (T_1^4-T_2^4)\psi _b}{1+\psi _b(1/\epsilon _1+1/\epsilon _2-2)} (11.66)
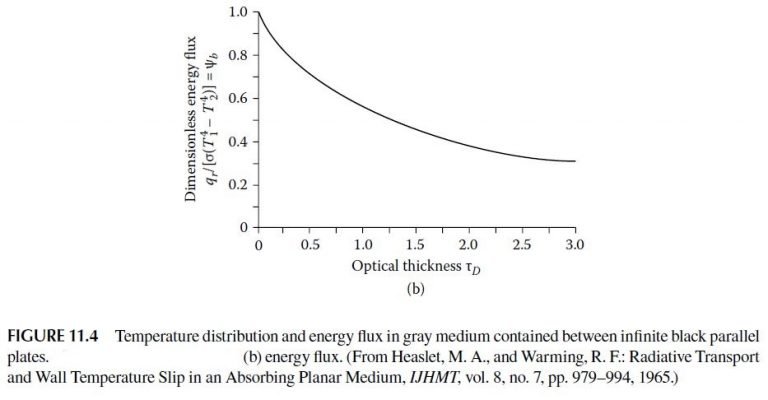
The ψ_b is in Figure 11.4b or Table 11.2, where \tau _D=\int_{0}^{D}{\sigma _s(x)} dx.
| TABLE 11.2 Dimensionless Energy Flux q_r/ \sigma(T_1^4-T_2^4)=ψ_b^a |
|||
| Optical Thickness τ_D | ψ_b | Optical Thickness τ_D | ψ_b |
| 0 | 1 | 0.8 | 0.6046 |
| 0.1 | 0.9157 | 1 | 0.5532 |
| 0.2 | 0.8491 | 1.5 | 0.4572 |
| 0.3 | 0.7934 | 2 | 0.39 |
| 0.4 | 0.7458 | 2.5 | 0.3401 |
| 0.5 | 0.704 | 3 | 0.3016 |
| 0.6 | 0.6672 | 4 | 0.246 |
| a For τ_D >> 1, ψ_b = (4/3)/(1.42089 + τ_D). Source: Heaslet, M. A., and Warming, R. F.: Radiative Transport and Wall Temperature Slip in an Absorbing Planer Medium, IJHMT, vol. 8, no. 7, pp. 979–994, 1965. |
|||
