Question 12.11: A shaft of diameter d, bent in the form of a semi-circle of ...
A shaft of diameter d, bent in the form of a semi-circle of radius R is built-in at A and loaded at B by a force P acting perpendicular to the plane of the shaft as shown in Figure 12.21. Find the value of angle \phi for which the principal stress \sigma_1 will be maximum.

Learn more on how we answer questions.
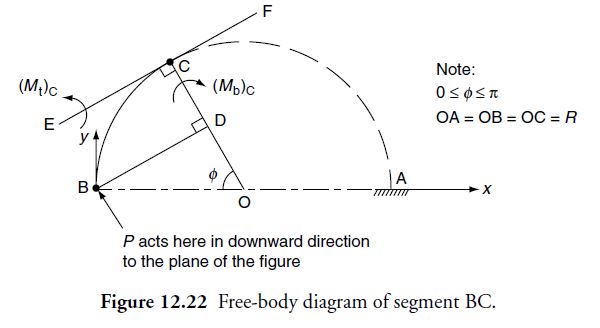
Let us draw the free-body diagram of the segment BC with angle \phi(0 \leq \phi \leq \pi) as shown in Figure 12.21, of the bent shaft in Figure 12.22.
From the foregoing free-body diagram shown in Figure 12.22, we observe at point C defined by the angle \phi(0 \leq \phi \leq \pi / 2) that the force and moment acting are as follows:
Force P vertically upward
Bending moment \left(M_{ b }\right)_{ C } about OC and
Torsional moment \left(M_{ t }\right)_{ C } about tangent EF drawn at C
Observe that EF and OC are perpendicular to each other at point C. Therefore,
\left(M_{ b }\right)_{ C }=P \cdot BD =P R \sin \phi \quad(\text { as from } \Delta OBD , \quad OB =R \quad \text { and } \quad BD \perp OD )
and \left(M_{ t }\right)_{ C }=P \cdot CD =P( OC – OD )=P R(1-\cos \phi) \quad(\text { as } OD =R \cos \phi)
So the principal stress \sigma_1 at C is defined as:
\sigma_1=\frac{\sigma_n}{2}+\sqrt{\left(\frac{\sigma_n}{2}\right)^2+\tau^2} (1)
where \sigma_n is the normal stress caused due to \left(M_{ b }\right)_{ C } is
\sigma_n=\frac{32\left(M_{ b }\right)_{ C }}{\pi d^3}
and τ is the shear stress caused due to \left(M_{ t }\right)_{ C }
\sigma_n=\frac{16\left(M_{ t }\right)_{ C }}{\pi d^3}
Putting these values in Eq. (1), we get:
\sigma_1=\left\lgroup \frac{16}{\pi d^3} \right\rgroup\left[\left(M_{ b }\right)_{ C }+\sqrt{\left(M_{ b }\right)_{ C }^2+\left(M_{ t }\right)_{ C }^2}\right]
Putting the expressions of \left(M_{ b }\right)_{ C } \text { and }\left(M_{ t }\right)_{ C } , we get:
\sigma_1=\left\lgroup \frac{16 P R}{\pi d^3} \right\rgroup \left[\sin \phi+\sqrt{\sin ^2 \phi+(1-\cos \phi)^2}\right]
=\left\lgroup \frac{16 P R}{\pi d^3} \right\rgroup [\sin \phi+\sqrt{2-2 \cos \phi}]
=\left\lgroup \frac{16 P R}{\pi d^3}\right\rgroup [\sin \phi+2 \sin (\phi / 2)]
Clearly \sigma_1 will be maximum when \sin \phi+2 \sin (\phi / 2) becomes maximum, that is, when
\frac{ d }{ d \phi}\left\lgroup \sin \phi+2 \sin \frac{\phi}{2} \right\rgroup =0
or \cos \phi+\cos \frac{\phi}{2}=0
or \cos \phi=-\cos \frac{\phi}{2}=\cos \left\lgroup \pi-\frac{\phi}{2} \right\rgroup
Therefore,
3 \phi=2 \pi \Rightarrow \phi=\frac{2 \pi}{3}=120^{\circ}
We check that the following differential is negative.
\left[\frac{ d ^2}{ d \phi^2}\left\lgroup \sin \phi+2 \sin \frac{\phi}{2} \right\rgroup\right]_{\phi=2 \pi / 3}
Hence \sin \phi+2 \sin (\phi / 2) is maximum when \phi=120^{\circ} . Thus, \sigma_1 the principal stress at C becomes maximum when \phi=120^{\circ} .