Question 5.5: A simply supported wood beam having a span length L = 3 m ca...
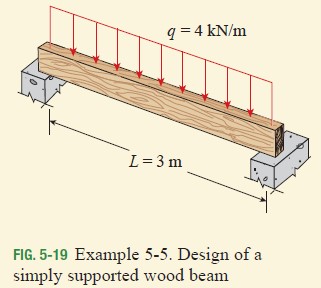
A simply supported wood beam having a span length L = 3 m carries a uniform load q = 4 kN/m (Fig. 5-19). The allowable bending stress is 12 MPa, the wood weighs 5.4 kN/m³, and the beam is supported laterally against sideways buckling and tipping.
Select a suitable size for the beam from the table in Appendix F (available online).
Learn more on how we answer questions.
Since we do not know in advance how much the beam weighs, we will proceed by trial-and-error as follows: (1) Calculate the required section modulus based upon the given uniform load. (2) Select a trial size for the beam. (3) Add the weight of the beam to the uniform load and calculate a new required section modulus. (4) Check to see that the selected beam is still satisfactory. If it is not, select a larger beam and repeat the process.
(1) The maximum bending moment in the beam occurs at the midpoint (see Eq. 4-15):
M_{max}=\frac{qL^2}{8} ( Eq. 4-15)
=\frac{(4 kN/m)(3 m)^2}{8 } =4.5 kN.m
The required section modulus (Eq. 5-24) is
S=\frac{M_{max}}{\sigma _{allow}} (Eq. 5-24)
=\frac{4.5 kN.m}{12 MPa}= 0.375 \times 10^6 mm^3
(2) From the table in Appendix F we see that the lightest beam that supplies a section modulus of at least 0.375 × 10^6 mm³ about axis 1-1 is a 75 × 200 mm beam (nominal dimensions). This beam has a section modulus equal to 0.456 × 10^6 mm³ and weighs 77.11 N/m (Note that Appendix F (available online) gives weights of beams based upon a density of 5.4 kN/m³.)
(3) The uniform load on the beam now becomes 4.077 kN/m, and the corresponding required section modulus is
S=(0.375 \times 10^6 mm^3)(\frac{4.077}{4.0} )= 0.382 \times 10^6 mm^3
(4) The previously selected beam has a section modulus of 0.456 × 10^6 mm³, which is larger than the required modulus of 0.382 × 10^6 mm³
Therefore, a 75 × 200 mm beam is satisfactory.
Note: If the weight density of the wood is other than 5.4 kN/m³, we can obtain the weight of the beam per linear foot by multiplying the value in the last column in Appendix F by the ratio of the actual weight density to 5.4 kN/m³.