Question 5.20: A Single-Link Robot Arm The mechanical model of a single-lin...

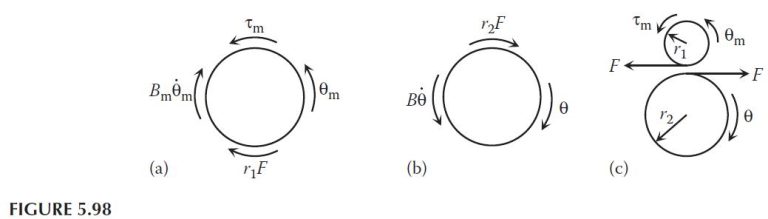
The free-body diagrams for the motor, the load, and the gear–train are shown in Figure 5.98, where F represents the contact force between the two gears. The moments caused by the contact force on the motor and on the load are r_1F and r_2F, respectively. Applying the moment equation to the motor and the load gives

+ \curvearrowleft : \sum M_O = I_O \alpha

τ_m – B_m\dot{θ}_m – r_1F = I_m\ddot{θ}_m

and

+ \curvearrowright : \sum M_O = I_O \alpha

– B_m\dot{θ} – r_2F = I_m\ddot{θ}

Solving for F from the equation for the load and substituting it into the equation for the motor results in

τ_m – B_m\dot{θ}_m – \frac{r_1}{r_2}(I\ddot{θ} + B\dot{θ}) I_m\ddot{θ}_m=

By the geometry of the gears,

\dot{θ} =\frac{r_1}{r_2}\dot{θ}_m = N\dot{θ}_m

\ddot{θ} =\frac{r_1}{r_2}\ddot{θ}_m = N\ddot{θ}_m

Substituting these into the previous differential equation gives

τ_m – B_m\dot{θ}_m – N^2 (I\ddot{θ}_m + B\dot{θ}_m) = I_m\ddot{θ}_m

which can be rearranged as

(I_m  N^2I)\ddot{θ}_m + (B_m + N^2B)\dot{θ}_m = τ_m

The equation is in terms of the angular displacement of the motor.