A single-stage gear train is shown in Figure 1. The input force Fin causes Shaft 1 to rotate counterclockwise. Gear 1 meshes with Gear 2 and causes Shaft 2 to rotate clockwise and exert the output force Fout on an output device (not shown). Each gear is mounted on a shaft of 5-mm radius supported

Question

ANALYSIS OF A FRICTIONLESS GEAR TRAIN²

A single-stage gear train is shown in Figure 1. The input force [latex]F_{in}[/latex] causes Shaft 1 to rotate counterclockwise. Gear 1 meshes with Gear 2 and causes Shaft 2 to rotate clockwise and exert the output force[latex]F_{out} [/latex] on an output device (not shown). Each gear is mounted on a shaft of 5-mm radius supported by journal bearings, as shown. The gear train is rotating at a constant rate. The gear diameters are [latex]r_{1}[/latex] = 25 mm and [latex]r_{2}[/latex] = 35 mm.
(a) Determine the ratio of output [latex]M_{out}[/latex] to input [latex]M_{in}[/latex] moments in terms of the diameters of various gears and shafts when the journal bearings are frictionless. This ratio is the mechanical advantage of this gear train. Also find the ratio for the particular case when [latex]r_{1}[/latex]= 25 mm and [latex]r_{2}[/latex] = 35 mm.
(b) Find the forces acting on the four journal bearings in terms of [latex]F_{in}[/latex].

Accepted Answer

Goal Find a relationship between the output and input moments when the gear train is in equilibrium. based on Figure 1, the requested ratio is [latex]M_{out} /M_{in} = r_{2} F_{out}/ r_{1}F_{in}[/latex] . In addition, find the loads at the journal bearings at A, B, C, and D in terms of [latex]F_{in}[/latex].
Given The geometry of the gear train and that the bearings are frictionless.
The input is via Gear 1, and the output is via Gear 2.
Assume The weight of various members that make up the gear train can be ignored and the journal bearings are frictionless (we will check this assumption in Example 9.2.4). because there must be a boundary connection to prevent the shafts from sliding in the x direction, and we are not told whether any of the bearings acts as a thrust bearing (Table 4.2), we arbitrarily assume that bearings B and D act as thrust bearings (and will check this assumption in our analysis).

²Gear trains are used in rotating systems to either increase or decrease moment or to decrease or increase rotational speed. In an automotive transmission, which is an example of a gear train, the moment from the engine (the input into the transmission) is increased and the rotational speed is decreased relative to the drive shaft (the output from the transmission). Often the input and output moments acting around a shaft are referred to as “torques.”

Draw We draw free-body diagrams for Shaft 1 and Shaft 2 in Figure 2. Notice that a third-law force pair acts between Gears 1 and 2.
Formulate Equations and Solve From the free -body diagram of Shaft 1 we can write:

[latex]M_{in} = (r_{1})(F_{in})[/latex]
[latex]\sum{M_{ x} }\left(\curvearrowleft + \right) =M_{in} - (r_{1})(F_{12}) =0[/latex]
[latex]F_{12} =\frac{M_{in}}{r_{1}} [/latex]

Similarly, from the free-body diagram of Shaft 2 we can write:

[latex]M_{out} = (r_{2})(F_{out})[/latex]
[latex]\sum{M_{x} }\left(\curvearrowleft + \right) =M_{out} - (r_{2})(F_{21}) =0[/latex]
[latex]F_{21} =\frac{M_{out}}{r_{2}} [/latex]

From Newton’s third law, we know that [latex]F_{12} = F_{21}[/latex] . Therefore, we can write:

[latex]M_{out} = r_{2}\frac{M_{in}}{r_{1}} [/latex]

Substituting in for [latex]r_{1}[/latex] = 25 mm and [latex]r_{2}[/latex] = 35 mm, we find that the requested ratio of [latex]M_{out}/M_{in}[/latex] is 1.4.

The mechanical advantage of the gear train is 1.4

Now we go about finding the forces acting at the bearings at A, B, C, and D, as requested in part (b) of this example.
We find the forces at A and B based on the free-body diagram for Shaft 1 by writing:

[latex]\sum{F_{x} \left(\rightarrow + \right) } = 0\Rightarrow F_{Ax}=0[/latex] (1)
[latex]\sum{M_{z @ B} }\left(\curvearrowleft + \right) =F_{in}r_{1}- F_{12}r_{1}=0[/latex] (2)

Therefore, [latex]F_{in} = F_{12}[/latex] (and we will use this finding in writing the next batch of equilibrium equations).

[latex]\sum{F_{y}\left(\uparrow + \right) } =- 2F_{in}+ F_{Ay}+F_{By} =0[/latex] (3)
[latex]\sum{F_{z}}=F_{Az}+F_{Bz} =0[/latex] (4)
[latex]\sum{M_{z @ B} }\left(\curvearrowleft + \right) = -2F_{in}a+ F_{Ay}\left(a+ a\right) =0[/latex]

From this set of equations, we find that:

[latex]F_{Ay}=F_{By}=F_{in}[/latex] and [latex]F_{Ax}=F_{Az}=F_{Bz}=0[/latex]

We find the forces at C and D based on the free-body diagram for Shaft 2 by writing:

[latex]\sum{M_{x @ D} }\left(\curvearrowleft + \right) =F_{out}r_{1}- F_{21}r_{1}=0[/latex] (5)

Therefore, [latex]F_{out}= F_{21}[/latex] . We also know from part (a), that [latex]F_{21}= F_{12}[/latex] , therefore, [latex]F_{out}= F_{in}[/latex] .

[latex]\sum{F_{x} \left(\rightarrow + \right) } = 0\Rightarrow F_{Cx}=0[/latex] (1)
[latex]\sum{F_{y}\left(\uparrow + \right) } =2F_{in}+F_{Cy} + F_{Dy}=0[/latex] (2)
[latex]\sum{F_{z}}=F_{Cz}+ F_{Dz}=0[/latex] (3)
[latex]\sum{M_{z @ D} }\left(\curvearrowleft + \right) =2F_{int}a+ F_{Cy}\left(a+ a\right) =0 [/latex]

From this set of equations, we find that:

[latex]F_{Cy}=F_{Dy}= - F_{in} [/latex] and [latex]F_{Cx}=F_{Cz}=F_{Dz}=0[/latex]

Check The general law for two (frictionless) gears is that the moment multiplies by the ratio of the gear diameters and the speed is decreased by the same ratio. This is what we found in our analysis!

Table 4.2 Standard Supports for Nonplanar Systems

(A)
Supports

Description of Boundary Loads

(B)
Loads to Be Shown in Free-Body Diagram

1. Normal contact without friction

Force (F) oriented normal to surface on which system rests. Direction is such that force pushes on system.

F

2. Cable, rope, wire

Force (F) oriented along cable. Direction is such that force pulls on system.

F

3. Spring

Force (F) oriented along long axis of spring. F Direction is such that force pulls on system if spring is in tension and pushes if spring is in compression.

F

4. Smooth roller in guide

Force represented as two components. One component ([latex] F_z [/latex]) normal to surface on which system rests; the other is perpendicular to rolling direction ([latex] F_x [/latex]).

[latex] F_x + F_z [/latex]

5. Normal contact with friction

Two forces, one ([latex] F_n [/latex]) oriented normal to surface so as to push on system, other force is tangent to surface on which the system rests and is represented in terms of its components ([latex] F_{fx} + F_{fy} [/latex]).

[latex] F_n [/latex]
[latex] F_{fx} + F_{fy} [/latex]

6. Ball and socket support
(ball or socket as part of system)

Force represented as three components

[latex] F_x + F_y + F_z [/latex]

7. Fixed support

Force represented in terms of components ([latex] F_x + F_y + F_z [/latex] ).
Moment represented in terms of components ([latex] M_x + M_y + M_z [/latex]).

[latex] F_x + F_y + F_z [/latex]

[latex] M_x + M_y + M_z [/latex]

8A. Single hinge
(shaft and articulated collar)

Force in plane perpendicular to shaft axis; represented as x and z components ([latex] F_x + F_z [/latex] ). Moment with components about axes perpendicular to shaft axis ([latex] M_x + M_z [/latex]). Depending on the hinge design, may also have a force component along axis of shaft, ([latex] F_y [/latex])

[latex] F_x + F_z [/latex]
[latex] M_x + M_z [/latex]

OR

[latex] F_x + F_y + F_z [/latex]

[latex] M_x + M_z [/latex]

8B. Multiple hinges
(one of two or more properly aligned hinges)

Force in plane normal to shaft axis represented in terms of components ([latex] F_x + F_z [/latex] ). Point of application at center of shaft. Depending on design, may also apply force component along axis of shaft ([latex] F_y [/latex]).

At hinge A: [latex] F_{Ax} + F_{Az} [/latex]
At hinge B: [latex] F_{Bx} + F_{Bz} [/latex]
OR
[latex] F_{Ax} + F_{Ay} + F_{Az} [/latex]
[latex] F_{Bx} + F_{By}+ F_{Bz} [/latex]

9A .Single journal bearing
(frictionless collar that holds a shaft)

Force in plane perpendicular to shaft axis; represented as x and z components ( [latex] F_x + F_z [/latex] ).
Moment with components about axes perpendicular to shaft axis ([latex] M_x + M_z [/latex])

[latex] F_x + F_z [/latex]
[latex] M_x + M_z [/latex]

9B. Multiple journal bearings
(two or more properly aligned journal bearings holding a shaft)

Force in plane perpendicular to shaft axis represented in terms of components ([latex] F_{Ax} + F_{Az} [/latex]). Point of application at center of shaft.

At journal bearing A: [latex] F_{Ax} + F_{Az} [/latex] At journal bearing A: [latex] F_{Bx} + F_{Bz} [/latex]

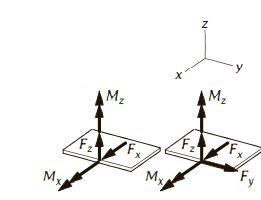
10A. Single thrust bearing
(journal bearing that also restricts motion along axis of shaft)

Force represented in terms of three components ([latex] F_x + F_z + F_y [/latex]). Component in direction of shaft axis ([latex] F_y [/latex]) is sometimes referred to as the “thrust force.” Point of application is at center of shaft. Moment with components perpendicular to shaft axis ([latex] M_x + M_z [/latex]).

[latex] F_x + F_y + F_z [/latex]
[latex] M_x + M_z [/latex]

10B. Multiple thrust bearings (one of two or more properly aligned thrust bearings)

Force represented in terms of three components ([latex] F_x + F_y + F_z [/latex]). Component in direction of shaft axis ([latex] F_y [/latex]) is sometimes referred to as the “thrust force.” Point of application is at center of shaft.

At thrust bearing A:
[latex] F_{Ax} + F_{Ay} + F_{Az} [/latex]

Question 9.2.3: A single-stage gear train is shown in Figure 1. The input fo...

Related Answered Questions

A toggle clamp holds workpiece F (Figure 1) (a) Assuming the weight of the clamp members can be ignored, determine the mechanical advantage of this toggle clamp, defined as the ratio of the output force at the workpiece to P.(b) For the dimensions shown in the accompanying list, what is the ...

Verified Answer:

For the frame configurations in Figure 1(a) and Figure 2 determine which of these labels apply to each frame: internally unstable, statically determinate, statically indeterminate, or underconstrained. ...

Verified Answer:

Reconsider the single-stage gear train shown in Figure 1 and described in Example 9.2.3 when the coefficient of kinetic friction associated with the journal bearings is 0.25. If r1 = 25 mm, r2 = 35 mm, and the diameter of the shafts is 5 mm, determine the mechanical advantage of the gear train. ...

Verified Answer:

Verified Answer:

Verified Answer:

Verified Answer:

Verified Answer:

The frame in Figure 1 is subjected to the force and moment shown. Assuming the weights of the frame members are negligible, find the loads acting on the frame at the supports at A and C. Also express these loads in terms of shear forces acting on pins A and C. ...

Verified Answer:

Identify each system in Figure 1 as either a truss or frame. Justify your answer. ...

Verified Answer: