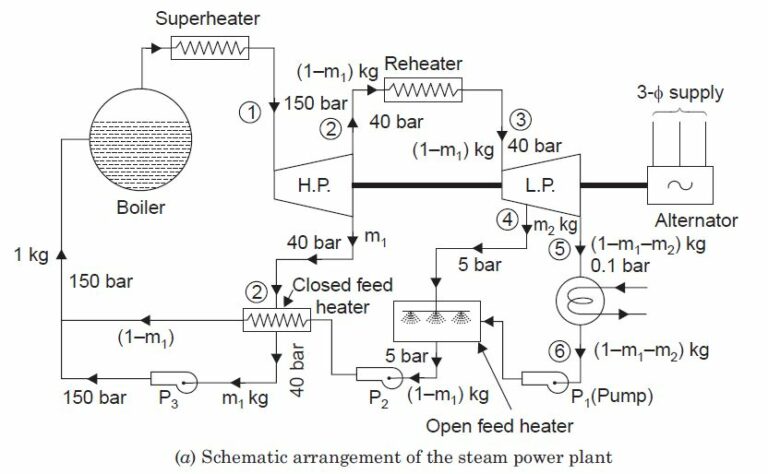
Question 12.26: A steam power plant operates on ideal Rankine cycle using re...
A steam power plant operates on ideal Rankine cycle using reheater and regenerative feed water heaters. It has one open feed heater. Steam is supplied at 150 bar and 600°C. The condenser pressure is 0.1 bar. Some steam is extracted from the turbine at 40 bar for closed feed water heater and remaining steam is reduced at 40 bar to 600°C. Extracted steam is completely condensed in this closed feed water heater and is pumped to 150 bar before mixing with the feed water heater. Steam for the open feed water heater is bled from L.P. turbine at 5 bar. Determine :
(i) Fraction of steam extracted from the turbines at each bled heater, and
(ii) Thermal efficiency of the system.
Draw the line diagram of the components and represent the cycle on T-s diagram.
Learn more on how we answer questions.
The arrangement of the components is shown in Fig. 12.41 (a) and the processes are represented on T-s diagram as shown in Fig. 12.41 (b).
From h-s chart and steam tables we have enthalpies at different points as follows :
\left.\begin{array}{ll}h_1=3578 \mathrm{~kJ} / \mathrm{kg} ; & h_2=3140 \mathrm{~kJ} / \mathrm{kg} ; \\h_3=3678 \mathrm{~kJ} / \mathrm{kg} ; & h_4=3000 \mathrm{~kJ} / \mathrm{kg} ; \\h_5=2330 \mathrm{~kJ} / \mathrm{kg} ; &\end{array}\right\} From h-s chart
\left.\begin{array}{rl}h_{f 1}(\text { at } 150 \mathrm{bar}) & =1611 \mathrm{~kJ} / \mathrm{kg} \\h_{f 2}(\text { at } 40 \mathrm{bar}) & =1087.4 \mathrm{~kJ} / \mathrm{kg} ; h_{f 4}(\text { at } 5 \mathrm{bar})=640.1 \mathrm{~kJ} / \mathrm{kg} ; \\h_{f 5} & =h_{f 6}(\text { at } 0.1 \mathrm{bar})=191.8 \mathrm{~kJ} / \mathrm{kg}\end{array}\right\} Steam tables
(i) Fraction of steam extracted from the turbines at each bled heater \mathrm{m}_1, \mathrm{~m}_2 :
Considering energy balance for closed feed heater, we have :
m_1\left(h_2-h_{f 2}\right)=\left(1-m_1\right)\left(h_{f 2}-h_{f 4}\right)m_1(3140-1087.4)=\left(1-m_1\right)(1087.4-640.1)
or 2052.6 m_1=\left(1-m_1\right) \times 447.3
∴ m _1=0.179 kg/kg of steam supplied by the boiler.
Considering energy balance for open feed heater, we have :
m_2\left(h_4-h_{f 4}\right)=\left(1-m_1-m_2\right)\left(h_{f_4}-h_{f 6}\right)or m_2\left(h_4-h_{f 4}\right)=\left(1-m_1-m_2\right)\left(h_{f 4}-h_{f 5}\right) \left(\because \quad h_{f 6}=h_{f 5}\right)
or m_2(3000-640.1)=\left(1-0.179-m_2\right)(640.1-191.8)
or 2359.9 m_2=\left(0.821-m_2\right) \times 448.3=368.05-448.3 m_2
∴ m _2=0.131 kg/kg of steam supplied by boiler.
(ii) Thermal efficiency of the system, \eta_{\text {thermal }} :
Total work done per kg of steam supplied by the boiler
=1 \times\left(h_1-h_2\right)+\left(1-m_1\right)\left(h_3-h_4\right)+\left(1-m_1-m_2\right)\left(h_4-h_5\right)= (3578 – 3140) + (1 – 0.179)(3678 – 3000) + (1 – 0.179 – 0.131)(3000 – 2330)
= 438 + 556.64 + 462.3 = 1456.94 kJ/kg
Work done by the pump P_1
W_{P 1}=v_{w 1}\left(1-m_1-m_2\right)(5-0.1) \times 10^5 \times 10^{-3} kJ/kg
= \frac{1}{1000}(1-0.179-0.131)(5-0.1) \times 10^5 \times 10^{-3}=0.338 kJ/kg
\left[\text { Taking } v_{w 1}=v_{w 2}=v_{w 3}=\frac{1}{1000} m ^3 / kg \right]Work done by the pump P_2,
W_{P 2}=v_{w 2}\left(1-m_1\right)(150-5) \times 10^5 \times 10^{-3} kJ/kg
= \frac{1}{1000}(1-0.179)(150-5) \times 10^5 \times 10^{-3}=11.9 kJ/kg
Work done by pump P_3,
W_{P 3}=v_{w 3} \times m_1 \times(150-40) \times 10^5 \times 10^{-3} kJ/kg
Total pump work =W_{P 1}+W_{P 2}+W_{P 3}
= 0.338 + 11.9 + 1.97 = 14.21 kJ/kg of steam supplied by boiler
∴ Net work done by the turbine per kg of steam supplied by the boiler,
W_{\text {net }}=1456.94-14.21=1442.73 kJ/kg
Heat of feed water extering the boiler
=\left(1-m_1\right) \times 1611+m_1 \times 1611=1611 kJ/kg
Heat supplied by the boiler per kg of steam,
Q_{s 1}=h_1-1610=3578-1610=1968 kJ/kg
Q_{s 2}= Heat supplied in the reheater
=\left(1-m_1\right)\left(h_3-h_\rho\right)=(1-0.179)(3678-3140)= 441.7 kJ/kg of steam supplied by the boiler
Q_{s t} (Total heat supplied) =Q_{s 1}+Q_{s 2}=1968+441.7=2409.7 kJ/kg
∴ \eta_{\text {thermal }}=\frac{W_{\text {net }}}{Q_{s t}}=\frac{1442.73}{2409.7}=0.5987 or 59.87%.