Question 10.SP.7: A steel column having an effective length of 16 ft is loaded...
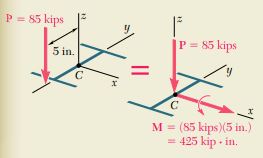
A steel column having an effective length of 16 \mathrm{ft} is loaded eccentrically as shown. Using the interaction method, select the wide-flange shape of 8-in. nominal depth that should be used. Assume E=29 \times 10^{6} psi and \sigma_{Y}=36 \mathrm{ksi}, and use an allowable stress in bending of 22 \mathrm{ksi}.

Learn more on how we answer questions.
So that we can select a trial section, we use the allowable-stress method with \sigma_{\text {all }}=22 \mathrm{ksi} and write
\sigma_{\text {all }}=\frac{P}{A}+\frac{M c}{I_{x}}=\frac{P}{A}+\frac{M c}{A r_{x}^{2}} (1)
From Appendix C we observe for shapes of 8 -in. nominal depth that c \approx 4 in. and r_{x} \approx 3.5 \mathrm{in}. Substituting into Eq. (1), we have
22 \mathrm{ksi}=\frac{85 \mathrm{kips}}{A}+\frac{(425 \mathrm{kip} \cdot \mathrm{in} .)(4 \mathrm{in} .)}{A(3.5 \mathrm{in} .)^{2}} \quad A \approx 10.2 \mathrm{in}^{2}
We select for a first trial shape: \mathrm{W} 8 \times 35.
Trial 1: W8 \times 35. The allowable stresses are
Allowable Bending Stress: (see data ) \quad\left(\sigma_{\text {all }}\right)_{\text {bending }}=22 \mathrm{ksi}
Allowable Concentric Stress: The largest slenderness ratio of the column is L / r_{y}=(192 \mathrm{in}) /.\left(2.03 \mathrm{in}\right..) =94.6. Using Eq. (10.41) with E=29 \times 10^{6} \mathrm{psi} and \sigma_{Y}=36 \mathrm{ksi}, we find that the slenderness ratio at the junction between the two equations for \sigma_{c r} is L / r=133.7. Thus, we use Eqs. (10.38) and (10.39) and find that \sigma_{c r}=22.5 \mathrm{ksi}. Using Eq. (10.42), the allowable stress is
\left(\sigma_{\text {all }}\right)_{\text {centric }}=22.5 / 1.67=13.46 \mathrm{ksi}
For the W8 \times 35 trial shape, we have
\frac{P}{A}=\frac{85 \mathrm{kips}}{10.3 \mathrm{in}^{2}}=8.25 \mathrm{ksi} \quad \frac{M c}{I}=\frac{M}{S_{x}}=\frac{425 \mathrm{kip} \cdot \mathrm{in} .}{31.2 \mathrm{in}^{3}}=13.62 \mathrm{ksi}
With this data we find that the left-hand member of Eq. (10.60) is
\frac{P / A}{\left(\sigma_{\text {all }}\right)_{\text {centric }}}+\frac{M c / I}{\left(\sigma_{\text {all }}\right)_{\text {bending }}}=\frac{8.25 \mathrm{ksi}}{13.46 \mathrm{ksi}}+\frac{13.62 \mathrm{ksi}}{22 \mathrm{ksi}}=1.232
Since 1.232>1.000, the requirement expressed by the interaction formula is not satisfied; we must select a larger trial shape.
Trial 2: W8 \times 48. Following the procedure used in trial 1, we write
\begin{gathered} \frac{L}{r_{y}}=\frac{192 \mathrm{in} .}{2.08 \mathrm{in} .}=92.3 \quad\left(\sigma_{\text {all }}\right)_{\text {centric }}=13.76 \mathrm{ksi} \\ \frac{P}{A}=\frac{85 \mathrm{kips}}{14.1 \mathrm{in}^{2}}=6.03 \mathrm{ksi} \quad \frac{M c}{I}=\frac{M}{S_{x}}=\frac{425 \mathrm{kip} \cdot \mathrm{in} .}{43.2 \mathrm{in}^{3}}=9.84 \mathrm{ksi} \end{gathered}
Substituting into Eq. (10.60) gives
\frac{P / A}{\left(\sigma_{\text {all }}\right)_{\text {centric }}}+\frac{M c / I}{\left(\sigma_{\text {all }}\right)_{\text {bending }}}=\frac{6.03 \mathrm{ksi}}{13.76 \mathrm{ksi}}+\frac{9.82 \mathrm{ksi}}{22 \mathrm{ksi}}=0.885<1.000
The W8 \times 48 shape is satisfactory but may be unnecessarily large.
Trial 3: W8 \times 40. Following again the same procedure, we find that the interaction formula is not satisfied.
Selection of Shape. The shape to be used is \quad W8 \times 48