Question 31.3: Ammonia is to be absorbed from an air mixture at 293 K and 1...
Ammonia is to be absorbed from an air mixture at 293 K and 1.013 \times 10^5 \mathrm{~Pa} pressure in a countercurrent packed tower, using water at 293 K as the absorbent. An inlet gas rate of 1.21 \times 10^{-2} \mathrm{~m}^3 / \mathrm{s} and an ammonia-free water rate of 9.46 \times 10^{-3} \mathrm{~kg} / \mathrm{s} will be used. If the ammonia, \mathrm{NH}_3, concentration is reduced from 3.52 to 1.29 % by volume, determine the ratio of \left(L_S / G_S\right)_{\text {actual }} /\left(L_S / G_S\right)_{\min }. Equilibrium data for the system at 293 K and .013 \times 10^5 . \mathrm{Pa} are as follows:
| \mathrm{X} \frac{\mathrm{kg} \mathrm{mol} \mathrm{NH}_3}{\mathrm{~kg} \mathrm{~mol} \mathrm{H}_2 \mathrm{O}} | 0.0164 | 0.0252 | 0.0349 | 0.0455 | 0.0722 |
| \mathrm{Y} \frac{\mathrm{kg} \mathrm{mol} \mathrm{NH}_3}{\mathrm{~kg} \mathrm{~mol} \mathrm{H}_2 \mathrm{O}} | 0.021 | 0.032 | 0.042 | 0.053 | 0.08 |
Learn more on how we answer questions.
The total moles of gas entering the tower per hour may be evaluated using the ideal gas law.
G_1 A=\text { moles entering gas } / \mathrm{s}=\frac{P \dot{V}}{R T}=\frac{\left(1.013 \times 10^5 \mathrm{~Pa}\right)\left(1.21 \times 10^2 \mathrm{~m}^2 / \mathrm{s}\right)}{\left(8.314 \frac{\mathrm{Pa} \cdot \mathrm{m}^3}{\mathrm{~mol} \cdot \mathrm{K}}\right)(293 \mathrm{~K})}=0.503 \mathrm{~mol} / \mathrm{s}
The gas enters the tower with a mole fraction of ammonia, \mathrm{Y}_{A_1}, equal to 0.0352. Choosing a cross-sectional area for the tower of A m², we may evaluate the moles of G on a solute-free basis as
G_S=G_1\left(1-y_{A 1}\right)=\left(0.503 \frac{\mathrm{mol}}{\mathrm{s}}\right)\left(\frac{0.9648}{A \mathrm{~m}^2}\right)=\frac{0.483}{A} \frac{\mathrm{mol}}{\mathrm{s} \cdot \mathrm{m}^2}The moles of phase L on a solute-free basis are
L_S=\left(9.46 \times 10^{-3} \frac{\mathrm{kg}}{\mathrm{s}}\right)\left(\frac{\mathrm{kg} \mathrm{mol}}{18 \mathrm{~kg}}\right)\left(\frac{1}{A \mathrm{~m}^2}\right)=\frac{5.26 \times 10^{-4}}{A} \frac{\mathrm{kg} \mathrm{mol}}{\mathrm{s} \cdot \mathrm{m}^2}=\frac{0.526}{A} \frac{\mathrm{mol}}{\mathrm{s} \cdot \mathrm{m}^2}The ratio of the actual L_S to G_S is evaluated as
\left(\frac{L_S}{G_S}\right)_{\text {actual }}=\frac{0.526}{A} \frac{A}{0.483}=1.09 \frac{\text { mole } \mathrm{NH}_{3 \text {-free }} L \text { phase }}{\text { mole } \mathrm{NH}_{3 \text {-free }} G \text { phase }}The composition of the known streams, G_1, G_2, and L_2 on a solute-free basis, are evaluated from the known mole fraction as
Y_{\mathrm{NH}_3, 1}=\frac{y_{\mathrm{NH}_3, 1}}{1-y_{\mathrm{NH}_3, 1}}=\frac{0.0352}{0.9648}=0.0365Y_{\mathrm{NH}_3, 2}=\frac{y_{\mathrm{NH}_3, 2}}{1-y_{\mathrm{NH}_3, 2}}=\frac{0.0129}{0.9871}=0.0131
X_{\mathrm{NH}_3, 2}=\frac{x_{\mathrm{NH}_3, 2}}{1-x_{\mathrm{NH}_3, 2}}=0
The exiting composition, X_{\mathrm{NH}_3, 1}, can be evaluated by
G_S\left(Y_{A_1}-Y_{A_2}\right)=L_S\left(X_{A_1}-X_{A_2}\right)\frac{0.483}{A}(0.0365-0.0131)=\frac{0.526}{A}\left(X_{A_1}-0\right)
X_{A_1}=0.0215
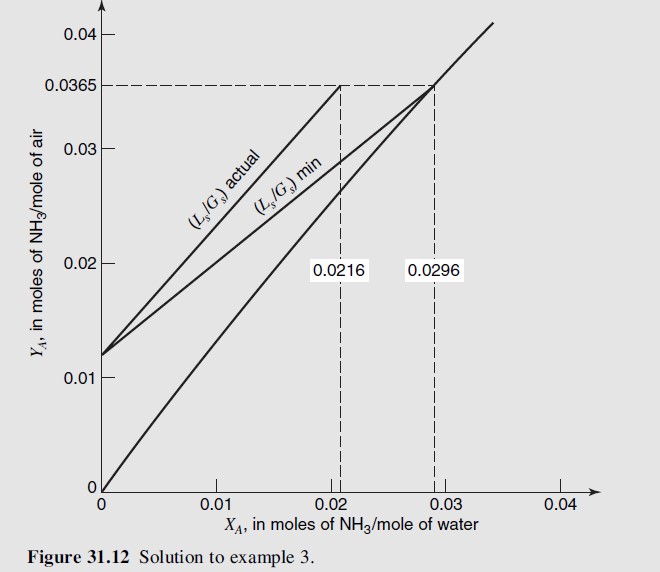
The actual and minimum operating lines are shown in Figure 31.12. The composition of the solution in equilibrium with Y_{\mathrm{NH}_3, 1}=0.0365 is obtained from the equilibrium curve as X_{\mathrm{NH}_{3, \text { equll }}}=0.0296. The slope of the minimum operating line is
\left(\frac{L_S}{G_S}\right)_{\text {minimum }}=\frac{\Delta Y}{\Delta X}=\frac{0.0365-0.0131}{0.0296-0}=0.79 \frac{\text { mole } \mathrm{NH}_{3 \text {-free }} \text { liquid phase }}{\text { mole } \mathrm{NH}_{3 \text {-free }} \text { gas phase }}The desired ratio, \left(L_S / G_S\right)_{\text {actual }} /\left(L_S / G_S\right)_{\text {minimum }} is then a ratio of the two values, 1.09/0.79 or 1.38.