Question 11.2.1: An electrical power line weighs 1 lb/ft and is anchored to t...
CATENARY CURVE WITH SUPPORTS AT SAME HEIGHT
An electrical power line weighs 1 lb/ft and is anchored to towers of the same height (Figure 1). The span between towers is 400 ft, and the maximum design sag is restricted to 80 ft. Determine the length of the cable and the maximum tension.

Learn more on how we answer questions.
Goal Find the length of the cable and the maximum tension.
Given Information about the geometry and weight of the power line as well as the maximum allowable sag.
Assume The cable is inextensible and the weight of the cable is the only significant loading.
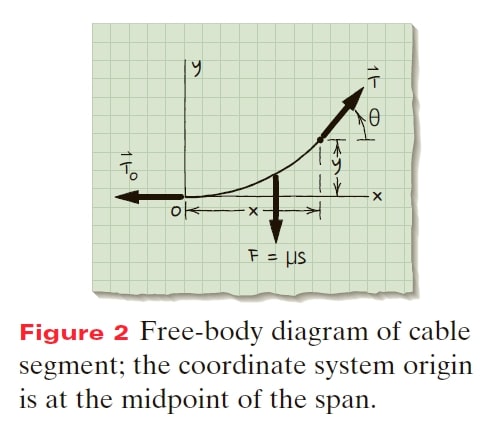
Draw because of symmetry, the lowest point in the cable occurs halfway between the two towers. This is where we locate the origin of the coordinate system on the free-body diagram (Figure 2) of a segment of the cable.
Formulate Equations and Solve Since the only significant load on the cable is its own weight, the cable will take on a catenary shape, and the equations developed under Case III are relevant. To determine the maximum tension in the cable we first determine the horizontal force in the cable, T_{O} , which we calculate using (11.1A):
y=\frac{T_{O}}{\mu } \left[cosh \frac{\mu x}{T_{O}} – 1 \right] (11.1A)
At the tower at B, x_{B}= 200 ft , y_{B}=80 ft , and \mu =1 lb/ft , therefore:
80 ft=\frac{T_{O}}{1 lb/ft} \left[cosh\left\lgroup\frac{1 lb/ft(200 ft)}{T_{O}} \right\rgroup – 1 \right]
We solve this equation using a trial-and-error approach with the result T_{O}= 262.3 lb.
using (11.2), we now solve for T_{max} at x = 200 ft, y = 80 ft:
T=T_{O} cosh \frac{\mu x}{T_{O}} \underbrace{=}_{using (11.1A)} T_{O} + \mu y (11.2)
T_{max}=T_{O} + \mu y = 262.3 lb + 1 lb/ft (80 ft) \Rightarrow T_{max}= 342 lb
This maximum tension occurs where the cable attaches to the towers and where its slope is the steepest.
We find the total cable length between the two towers by using (III.5), remembering that tower A is at (−200 ft, 80 ft) and tower B is at (200 ft, 80 ft):
L = – s_{OA} + s_{OB}= \frac{T_{O}}{\mu } \left[- \sin h \left\lgroup \frac{\mu x_{A}}{T_{O}} \right\rgroup + \sin h \left\lgroup\frac{\mu x_{B}}{T_{O}}\right\rgroup\right] (III.5)
L = \frac{262.3 lb}{1 lb/ft} \left[- \sin h\left\lgroup\frac{1 lb/ft(- 200 ft)}{262.3 lb} \right\rgroup + \sin h \left\lgroup\frac{1 lb/ft(200 ft)}{262.3 lb} \right\rgroup \right] \Rightarrow L =440 ft
Check Aside from rechecking calculations, there are no alternative calculations that serve as a check for this problem.