Question 12.7: Analog Computer Simulation of Automotive Suspension Implemen...
Analog Computer Simulation of Automotive Suspension
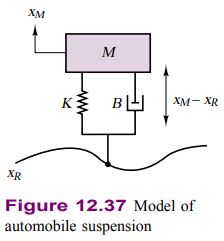
Implement the analog computer simulation of the automotive suspension system of Figure 12.37.
Learn more on how we answer questions.
Known Quantities: Mass, spring rate, and damping parameters of automotive suspension.
Find: Component values of analog computer circuit of Figure 12.39.
Schematics, Diagrams, Circuits, and Given Data: M=400 \mathrm{~kg} ; K=1.6 \times 10^{5} \mathrm{~N} / \mathrm{m}; B=20 \times 10^{3} \mathrm{~N} / \mathrm{m}-\mathrm{s}.
Assumptions: Assume ideal op-amps. Express all resistors in \mathrm{M} \Omega and all capacitors in \mu \mathrm{F}.
Analysis: With reference to Figure 12.39, we observe that the analog computer simulation of the automotive suspension requires: a four-input summer, two integrators, two coefficient multipliers, and one sign inverter.
Expressing all resistors in \mathrm{M} \Omega and all capacitors in \mu \mathrm{F} is useful because each integrator has a multiplier of -1 / R C. Using R=1 \mathrm{M} \Omega and C=1 \mu \mathrm{F} results in -1 / R C=-1. Figure 12.40 depicts the integrator configuration. The four-input summing amplifier uses 1-\mathrm{M} \Omega resistors throughout, so that the gain for each input is also equal to -1. On the other hand, the two coefficient multipliers are required to have gains -K / M=-4,000 and -B / M=50, respectively. Thus we select 10-\mathrm{M} \Omega and 2.5-\mathrm{k} \Omega resistors for the first coefficient multiplier, and 1-M \Omega and 20-k \Omega resistors for the second. Finally, the inverter can be realized with two 1-M \Omega resistors. The various elements are depicted in Figure 12.40.
Comments: Note that it is not necessary to employ five op-amps in this analog simulator. The summing amplifier function and the first integrator could, for example, be combined into a single op-amp, and one of the two coefficient multipliers could be eliminated. This idea is explored further in the homework problems.

