Question 11.4: Analysis of a Planetary Gear Train In the epicyclic gear tra...
Analysis of a Planetary Gear Train
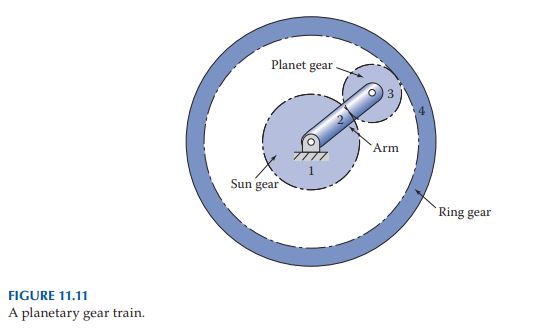
In the epicyclic gear train illustrated in Figure 11.11, the sun gear is driven clockwise at 60 rpm and has N_{1} teeth, the planet gear N_{3} teeth, and the ring gear N_{4} teeth. The sun gear is the input and the arm is the output. The ring gear is held stationary. What is the velocity of the arm?
Given: N_{1} = 30, N_{3} = 20, N_{4} = 80.
Assumption: The sun gear is the first gear in the train and the ring gear is the last.
Refer to Figure 11.11.
The gear value, through the use of Equation 11.17, is
e = \pm \frac{\text {Product of number of teeth on driver gears}}{\text {Product of number of teeth on driver gears}} (11.17)
e=\left(-\frac{N_1}{N_3}\right)\left(+\frac{N_3}{N_4}\right)=\left(-\frac{30}{20}\right)\left(+\frac{20}{80}\right)=-0.375
Observe the signs on the gearset ratios: One is an external set (−) and one an internal set (+). Substitution of this equation together with n_{F} = n_{1} = 60 rpm and n_{L} = n_{4} = 0 into Equation 11.18 gives
e=\frac{n_L-n_A}{n_F-n_A} (11.18)
-0.375=\frac{n_4-n_2}{n_1-n_2}=\frac{0-n_2}{60-n_2}
from which n_{2} = 16.4 rpm.
Comment: The sun gear rotates 3.66 times as fast and in the same direction as the arm.