Question 5.12: Analysis of a Wye–Wye System A balanced positive-sequence wy...

Solution First, by computing the complex impedance of each phase of the load, we find that

Z=R+j\omega L=50+j2\pi(60)(0.1)=50+j37=62.62\angle 37.02^\circ

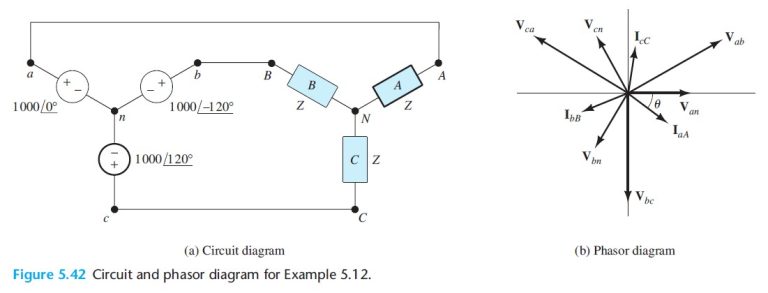
Next, we draw the circuit as shown in Figure 5.42(a). In balanced wye–wye calculations, we can assume that n and N are connected. (The currents and voltages are the same whether or not the neutral connection actually exists.) Thus, V_an appears across phase A of the load, and we can write

\mathrm{I}_{aA}=\frac{\mathrm{V}_{an}}{Z}=\frac{1000\angle 0^\circ}{62.62\angle 37.02^\circ}=15.97\angle -37.02^\circ

Similarly,

\mathrm{I}_{bB}=\frac{\mathrm{V}_{bn}}{Z}=\frac{1000\angle -120^\circ}{62.62\angle 37.02^\circ}=15.97\angle -157.02^\circ

\mathrm{I}_{cC}=\frac{\mathrm{V}_{cn}}{Z}=\frac{1000\angle 120^\circ}{62.62\angle 37.02^\circ}=15.97\angle 82.98^\circ

We use Equations 5.103, 5.104, and 5.105 to find the line-to-line phasors:

\mathrm{V}_{ab}=\mathrm{V}_{an}\times \sqrt{3}\angle 30^\circ=1732\angle 30^\circ

\mathrm{V}_{bc}=\mathrm{V}_{bn}\times \sqrt{3}\angle 30^\circ=1732\angle -90^\circ

\mathrm{V}_{ca}=\mathrm{V}_{cn}\times \sqrt{3}\angle 30^\circ=1732\angle 150^\circ

The power delivered to the load is given by Equation 5.94:

p(t)=3\frac{V_YI_L}{2}\cos{(\theta)}=3 \left(\frac{1000\times 15.97}{2} \right) \cos{(37.02^\circ)}=19.13\mathrm{~kW}

The reactive power is given by Equation 5.98:

Q=3\frac{V_YI_L}{2}\sin{(\theta)}=3V_{Y\mathrm{rms}}I_{L\mathrm{rms}}\sin{(\theta)}             (5.98)

Q=3\frac{V_YI_L}{2}\sin{(\theta)} =3 \left(\frac{1000\times 15.97}{2} \right) \sin{(37.02^\circ)}=14.42\mathrm{~kVAR}

The phasor diagram is shown in Figure 5.42(b). As usual, we have chosen a different scale for the currents than for the voltages.