Question 2.6.2: Briefly explain the basis of the method of joints for static...

If there are j joints in a truss, then since there are two equations ( \sum{P_{x}=0};\sum{P_{y}=0}) to each joint, there will be a total of 2j equations. If the truss is supported on a hinge and a roller, such as the one in Fig. 2.6-1 (a), the unknowns are the m member forces and the three reaction components. Since Eqn 2.5-1 states that

m + 3 = 2j
the number of equations will be exactly equal to the number of unknowns. If the truss is connected to the foundation by three bars, as in Figs. 2.5-4 and 2.5-5, then the total number of unknowns is w, where m now includes the three bars which hold the truss to the foundation. In this case, the member-joint relationship (Eqn 2.5-2) is
m = 2j

so that there are again exactly as many equations as there are unknowns.

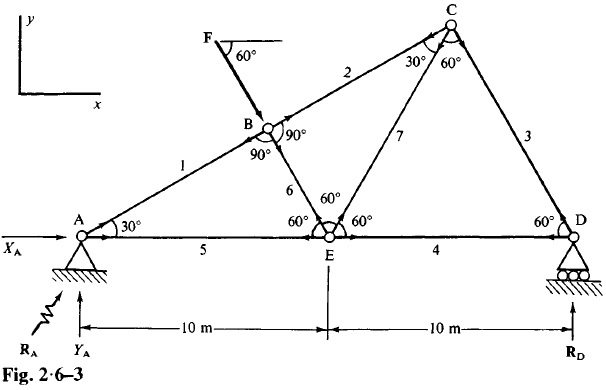
Note, however, that while it is always possible to set up the 2j equations and solve them formally, it is rarely desirable to do so. Instead, we should first try to determine those member forces which can be found by inspection or by very little calculation. With as many as possible of such readily determined forces calculated, the number of simultaneous equations that have to be solved is greatly reduced. Indeed, in many cases, it is not even necessary to solve more than two simultaneous equations. This point will be made clear by the following calculations for the truss in Fig. 2.6-1 (a), which, for clarity, has been redrawn again as Fig. 2.6-3.
Let S_{1} to S_{7}  inclusive be the (assumed) tensile forces in members 1 to 7 respectively. Let X_{A}  and Y_{A}  be the x- and y-components of the support reaction at A, i.e. R_{A}=\begin{bmatrix} X_{A} & Y_{A}  \end{bmatrix}^{T}; let R_{D}  be the support reaction at D which is known to be in the y-direction.

STEP 1: Consider equilibrium of whole truss (Fig. 2.6-3). \sum{ M} = 0 at joint A gives

Then

\sum{P_{y}} =0  gives

where R_{D}   is already known, then

\sum{P_{x}} =0  gives

hence

Note: It could have been written down by inspection that Y_{A} = R_{D} =0.433F and that X_{A} = -0.5F. The line of action of the force F passes through B and E; hence F at B can be replaced by a force F at E, for the purpose (only) of determining the support reactions. A force F at E inclined at 60° to the horizontal, is equivalent to a horizontal component of F cos 60° and a vertical component of F sin 60°, both applied at joint E. The horizontal component F cos 60° is resisted entirely by support A; hence X_{A} = -0.5F. The vertical component is resisted equally by supports A and D; hence Y_{A}  = R_{D} = 0.5F \sin \ 60° = 0.433F.

STEP 2: Equilibrium of joint A. Condition \sum{P_{y}} =0  gives

where Y_A is 0.433F(from Step 1). Then

(The negative sign for S_1 indicates that member 1 is actually in compression, and not in tension as assumed.) Conditio \sum{P_{x}} =0  gives

Where X_A = -0.5F \ and \ S_1 = -0.866F. Then

STEP 3: Equilibrium of joint B. For equilibrium in direction BC, since S_2 = S_1,

\qquad  S_2= \underline{-0.866F}

For equilibrium in direction BE, since S_6 + F =0 ,

\qquad S_6 = \underline{-F}

STEP 4: Equilibrium of joint D. Conditio \sum{P_{y}}=0 gives

where R_{D}  = 0.433F (from Step 1). Then
\qquad S_3 =\underline{-0.5F}
Conditio \sum{P_{x}}=0 gives
\qquad S_4 + S_3 \cos \ 60° = 0 \\ \qquad S_4 = \underline{0.25F,} \hspace{2em} since \hspace{3em} S_3 = -0.5F
STEP 5: Equilibrium of joint C. For equilibrium in direction CB, we must have
\qquad S_2 + S_7 \cos 30° = 0
where S_2 = -0.866F (from Step 3). Then

Forces S_1 \ to \ S_7  inclusive are now all determined. As a check, consider equilibrium of joint E.

Condition \sum{P_{x}}=0 demands that

which is identically satisfied for the values of S_7, S_4, S_6, \ and \ S_5 calculated above. Condition \sum{P_{y}}=0 demands that

which is again identically satisfied.