Question 6.4.3: Calculate Ix and Iy for the T-section with respect to the ce...
MOMENT OF INERTIA OF A COMPOSITE AREA
Calculate I_{x} and I_{y} for the T-section with respect to the centroidal axes shown in Figure 1.

Learn more on how we answer questions.
Goal Find I_{x} and I_{y} for the defined T-section.
Given Dimensions of the T-section, location of its centroid, and a coordinate system.
Assume No assumptions needed.
Draw We divide the T-section into two rectangles and identify the centroid for each one (Figure 2).
Formulate Equations and Solve We find the moment of inertia of the composite section by finding I_{x} and I_{y} for each rectangle and summing them.
I_{x}=I_{1x}+ I_{2x} and I_{y}=I_{1y}+ I_{2y}
Table C.1 gives the moment of inertia for a rectangle about axes through its centroid. For each rectangle we need to use the parallel axis theorem (6.28A) to find the moment of inertia about the x axis.
I_{x}= I_{x_{C}}+ A\left(y_{1} \right) ^{2} (6.28A)
I_{ix}= I_{x_{Ci}}+ Ax^{2}_{1i}
Since the y axis of the T-section coincides with the centroidal y axes for both of the rectangles we do not need the parallel axis theorem for I_{y}. We use a tabular format for our calculations to keep the calculations organized:
| Rectangle | Area in.² |
I_{x_{C}} in.^{4} |
y_{1} in. |
Ay^{1}_{2} in.^{4} |
I_{y_{C}} in.^{4} |
| 1 | 36 | 12 | 5 | 900 | 972 |
| 2 | 36 | 972 | 5 | 900 | 12 |
| ∑ | 984 | 1,800 | 984 |
I_{x}= \sum{I_{ix}} = \sum{I_{x_{Ci}}} + \sum{Ay_{1i^{2}}} = 984 in.^{4} + 1,800 in.^{4}=2, 784 in.^{4}
I_{y}=\sum{I_{iy}}= 984 in.^{4}
Check There is no easy way to check our solution, but we could use (6.26A) and (6.26B) and integrate to find I_{x}and I_{y}.
I_{x}=\int_{area}^{}{y^{2} dA} (6.26A)
I_{y}=\int_{area}^{x}{x^{2} dA} (6.26B)
Table C.1 Areas, Centroids, and Area Moments of Inertia
| Shape | Area Moment of inertia |
 |
I_{xc} = \frac{bh^{3}}{12}
I_{yc} = \frac{b^{3}h}{12} I_{x} = \frac{bh^{3}}{3}
I_{y} = \frac{b^{3}h}{3} |
 |
I_{xc} = \frac{bh^{3}}{36}
I_{yc} = \frac{b^{3}h}{36} I_{x} = \frac{bh^{3}}{12}
I_{y} = \frac{b^{3}h}{12} |
 |
I_{xc} = \frac{bh^{3}}{36}
I_{yc} = \frac{bh}{36} (b^{2} +c^{2} -bc)
I_{x} = \frac{bh^{3}}{12} |
 |
I_{xc} =I_{yc} = \frac{1}{4}\pi r^{4} |
 |
I_{xc} =I_{yc} = \left\lgroup\frac{\pi }{16} – \frac{4}{9\pi } \right\rgroup r^{4}
I_{x} =I_{y} = \frac{\pi r^{4}}{16} |
 |
I_{xc} =\frac{r^{4}}{\pi} \left\lgroup\alpha – \frac{\sin 2\alpha }{2} \right\rgroup
I_{yc} = \frac{r^{4}}{\pi} \left\lgroup\alpha + \frac{\sin 2\alpha }{2} \right\rgroup |
 |
|
 |
I_{xc} =\frac{\pi}{4} ab^{3}
I_{yc} = \frac{\pi}{4} a^{3} b |
 |
I_{xc} =\left\lgroup\frac{9\pi ^{4}- 64}{144\pi } \right\rgroup ab^{3}
I_{yc} = \left\lgroup\frac{9\pi ^{4}- 64}{144\pi } \right\rgroup a^{3} b |
 |
I_{xc} =\frac{8}{175} ab^{3}
I_{yc} = \frac{19}{480} a^{3} b |
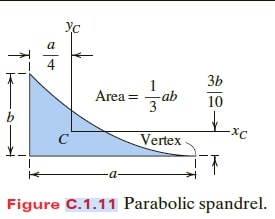 |
I_{xc} =\frac{19}{1050} ab^{3}
I_{yc} = \frac{1}{80} a^{3} b |
