Question 6.4.2: Calculate Ix, Iy, rx and ry for the right triangle shown in ...
MOMENT OF INERTIA USING PARALLEL AXIS THEOREM
Calculate I_{x} , I_{y} , r_{x} and r_{y} for the right triangle shown in Figure 1.

Learn more on how we answer questions.
Goal Find the (a) moment of inertia and (b) the radius of gyration about the x and y axes for the defined right triangle.
Given Dimensions of the triangle, location of its centroid, and a coordinate system.
Assume No assumptions needed.
Draw No drawing needed.
Formulate Equations and Solve (a) A triangle is a standard shape whose properties are tabulated in Appendix C. From Table C.1 we find the area of the triangle and its moment of inertia about x and y axes through the centroid.
A=\frac{ab}{2}
I_{xc}=\frac{ab^{3}}{36}
I_{yc}=\frac{a^{3}b}{36}
We then use the parallel axis theorem (6.28A) to determine the moment of inertia about the x axis. The x axis is at distance y_{1} = 2b/3 from the centroidal x axis.
I_{x}= I_{x_{C}}+ A\left(y_{1} \right) ^{2} (6.28A)
I_{x}=I_{xc}+ Ay^{2}_{1}=\frac{ab^{3}}{36}+\frac{ab}{2}\left\lgroup\frac{2b}{3}\right\rgroup ^{2} = \frac{ab^{3}}{4}
Similarly, we use (6.28B) to determine the moment of inertia about the y axis, which is at distance x_{1} = a/3 from the centroidal y axis.
I_{y}= I_{y_{C}}+ A\left(x_{1} \right) ^{2} (6.28B)
I_{y}=I_{yc}+ Ax^{2}_{1}=\frac{a^{3}b}{36}+ \frac{ab}{2}\left\lgroup\frac{a}{3}\right\rgroup ^{2} =\frac{a^{3}b}{12}
(b) We use the results from (a), (6.29A) and (6.29B) to determine the radii of gyration.
r_{x}=\sqrt{\frac{I_{x}}{A} } =\sqrt{\frac{{ab^{3}}/{4}}{{ab}/{2}} } =\sqrt{\frac{3b^{2}}{2} } =b\sqrt{\frac{3}{2} }
r_{y}=\sqrt{\frac{I_{y}}{A} }=\sqrt{\frac{{a^{3}b}/{12}}{{ab}/{2}} } = \sqrt{\frac{a^{2}}{6} }=\frac{a}{\sqrt{6} }
Check I_{y} is tabulated in Table C.1, and our result agrees with the table. We could use (6.26A) and integrate to check I_{x} .
I_{x}=\int_{area}^{}{y^{2} dA} (6.26A)
Table C.1 Areas, Centroids, and Area Moments of Inertia
| Shape | Area Moment of inertia |
 |
I_{xc} = \frac{bh^{3}}{12}
I_{yc} = \frac{b^{3}h}{12} I_{x} = \frac{bh^{3}}{3}
I_{y} = \frac{b^{3}h}{3} |
 |
I_{xc} = \frac{bh^{3}}{36}
I_{yc} = \frac{b^{3}h}{36} I_{x} = \frac{bh^{3}}{12}
I_{y} = \frac{b^{3}h}{12} |
 |
I_{xc} = \frac{bh^{3}}{36}
I_{yc} = \frac{bh}{36} (b^{2} +c^{2} -bc)
I_{x} = \frac{bh^{3}}{12} |
 |
I_{xc} =I_{yc} = \frac{1}{4}\pi r^{4} |
 |
I_{xc} =I_{yc} = \left\lgroup\frac{\pi }{16} – \frac{4}{9\pi } \right\rgroup r^{4}
I_{x} =I_{y} = \frac{\pi r^{4}}{16} |
 |
I_{xc} =\frac{r^{4}}{\pi} \left\lgroup\alpha – \frac{\sin 2\alpha }{2} \right\rgroup
I_{yc} = \frac{r^{4}}{\pi} \left\lgroup\alpha + \frac{\sin 2\alpha }{2} \right\rgroup |
 |
|
 |
I_{xc} =\frac{\pi}{4} ab^{3}
I_{yc} = \frac{\pi}{4} a^{3} b |
 |
I_{xc} =\left\lgroup\frac{9\pi ^{4}- 64}{144\pi } \right\rgroup ab^{3}
I_{yc} = \left\lgroup\frac{9\pi ^{4}- 64}{144\pi } \right\rgroup a^{3} b |
 |
I_{xc} =\frac{8}{175} ab^{3}
I_{yc} = \frac{19}{480} a^{3} b |
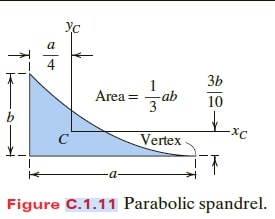 |
I_{xc} =\frac{19}{1050} ab^{3}
I_{yc} = \frac{1}{80} a^{3} b |