Question 5.s-5: Choosing an Alternative Using Expected Value with a Decision...
Choosing an Alternative Using Expected Value with a Decision Tree
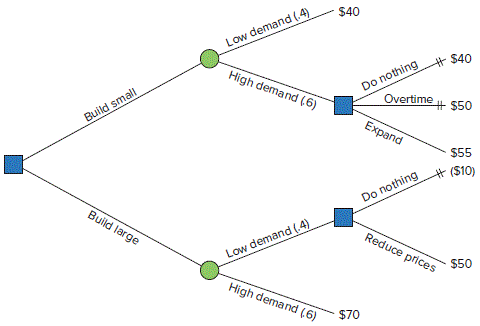
A manager must decide on the size of a video arcade to construct. The manager has narrowed the choices to two: large or small. Information has been collected on payoffs, and a decision tree has been constructed. Analyze the decision tree and determine which initial alternative (build small or build large) should be chosen in order to maximize expected monetary value.
Learn more on how we answer questions.
The dollar amounts at the branch ends indicate the estimated payoffs if the sequence of chance events and decisions that is traced back to the initial decision occurs. For example, if the initial decision is to build a small facility and it turns out that demand is low, the payoff will be $40 (thousand). Similarly, if a small facility is built, demand turns out to be high, and a later decision is made to expand, the payoff will be $55 (thousand). The figures in parentheses on branches leaving the chance nodes indicate the probabilities of those states of nature. Hence, the probability of low demand is .4, and the probability of high demand is .6. Payoffs in parentheses indicate losses.
Analyze the decisions from right to left:
1. Determine which alternative would be selected for each possible second decision. For a small facility with high demand, there are three choices: do nothing, work overtime, and expand. Because expand has the highest payoff, you would choose it. Indicate this by placing a double slash through each of the other alternatives. Similarly, for a large facility with low demand, there are two choices: do nothing and reduce prices. You would choose reduce prices because it has the higher expected value, so a double slash is placed on the other branch.
2. Determine the product of the chance probabilities and their respective payoffs for the remaining branches:
Build small
Low demand .4($40) = $16
High demand .6($55) =\frac{\$33}{\$49}
Build large
Low demand .4($50) = $20
High demand .6($70) =\frac{\$42}{\$62}
3. Hence, the choice should be to build the large facility because it has a larger expected value than the small facility.