Question 10.5.3: Consider the unbiased random walk on {1, 2, 3, 4, 5} with ab...

Linear Algebra and Its Applications

Consider the unbiased random walk on {1, 2, 3, 4, 5} with absorbing boundaries studied in Example 1. Find the probability that the chain is absorbed into state 1 given that the chain starts at state 4.

The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.

Placing the states in the order {1, 2, 3, 4, 5} gives the canonical form of the transition matrix:

\text { The matrix } Q \text { and the fundamental matrix } M=(I-Q)^{-1} \text { are }

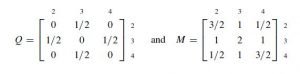
so

A=S M=\left[\begin{array}{ccc}1 / 2 & 0 & 0 \\0 & 0 & 1 / 2\end{array}\right]\left[\begin{array}{ccc}3 / 2 & 1 & 1 / 2 \\1 & 2 & 1 \\1 / 2 & 1 & 3 / 2\end{array}\right]

The columns of A correspond to the transient states 2, 3, and 4 in that order, while the rows correspond to the absorbing states 1 and 5. The probability that the chain that started at state 4 is absorbed at state 1 is 1/4.

Related Answered Questions

Question: 10.6.P.1

Let A be the matrix just before Example 1. Explain why entry (3, 6) is zero. ...

Verified Answer:

For entry (3,6) of A, the probability of a transit...

Question: 10.6.3

When the Atlanta Braves data from Example 2 is used to construct the transition matrix (not shown here), it turns out that the sum of the first column of the fundamental matrix M is 4:5048, and the first column of the matrix SM is [ .3520 .3309 .2365 .0805 ] Compute the number of earned runs the ...

Verified Answer:

The first column of SM shows that, for example, th...

Question: 10.6.4

Table 4 shows the career batting statistics for Jose Oquendo, who played for the New York Mets and St. Louis Cardinals in the 1980s and 1990s. Compute his offensive earned run average. ...

Verified Answer:

Construct the transition matrix from this data as ...

Question: 10.6.1

a. Justify the transition probabilities for the initial state “no bases occupied.” b. Justify the transition probabilities for the initial state “second base occupied.” ...

Verified Answer:

a. For the first column of A, the batter either ad...

Question: 10.6.2

Batting statistics are often displayed as in Table 3. Use the data in Table 3 to obtain the transition probabilities for the 2002 Atlanta Braves. ...

Verified Answer:

The sum of the entries in Table 3 is 6107. This is...

Question: 10.6.P.2

Explain why entry (6, 3) of A is .5p1. ...

Verified Answer:

For entry (6, 3) of A, the probability of a transi...

Question: 10.5.P.2

Consider a Markov chain on {1, 2, 3, 4} with transition matrix P = [ 2/3 1/2 0 0 1/3 1/6 1/2 0 0 1/3 1/6 1/2 0 0 1/3 1/2 ] a. If the Markov chain starts at state 2, find the expected number of steps required to reach state 4. b. If the Markov chain starts at state 2, find the probability that state ...

Verified Answer:

a. Reorder the states as {4, 1, 2, 3} and make sta...

Question: 10.5.P.1

Consider a Markov chain on {1, 2, 3, 4} with transition matrix P = [ 1 1/2 0 0 0 1/6 1/2 0 0 1/3 1/6 0 0 0 1/3 1 ] a. If the Markov chain starts at state 2, find the expected number of steps before the chain is absorbed. b. If the Markov chain starts at state 2, find the probability that the chain ...

Verified Answer:

a. Since states 1 and 4 are absorbing states, reor...

Question: 10.5.4

Consider a simple random walk on the graph in Figure 1. What is the probability that a walker starting at state 1 visits state 4 before visiting state 7? ...

Verified Answer:

Changing state 4 and state 7 to absorbing states a...

Question: 10.5.2

Consider an unbiased random walk on {1, 2, 3, 4, 5} with reflecting boundaries. Find the expected number of steps tj 4 required to get to state 4 starting at any state j ≠ 4 of the chain. ...

Verified Answer:

The transition matrix for this Markov chain is [la...