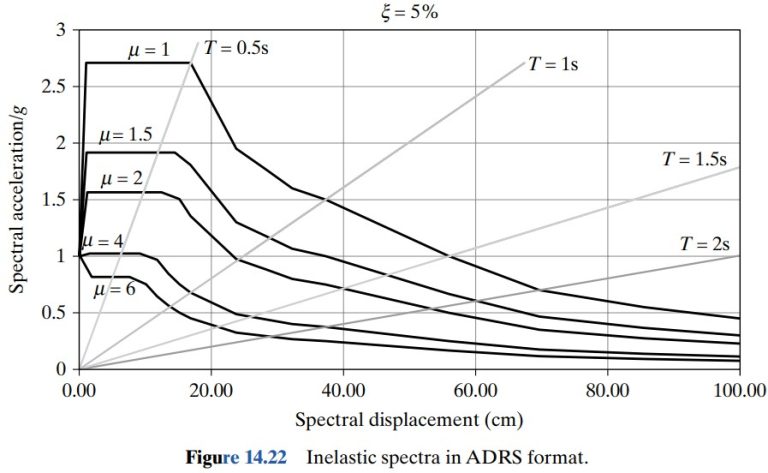
Construct an ADR spectrum for ductility ratio of 1, 1.5, 2, 4 and 6 for a ground motion having peak ground acceleration, peak ground velocity and peak ground displacement as 1 g, 90 cm/sec and 60 cm, respectively. Make use of Newmark–Hall amplification factors for 5% damping and 84.1 percentile.

Question

Accepted Answer

The inelastic response spectra for this ground motion for ductility ratio of 1.5, 2, 4 and 6 were developed in Example 13.5. An alternative format was shown in Example 13.6. The same data was used to develop the ADRS. The reduction factor R depends upon the acceleration or velocity-sensitive regions given by Equation (14.31). The spectral displacements are computed using Equation (14.32). Typical calculations for generating inelastic ADRS are shown in Table 14.8. Similar calculations can be done for other ductility ratios. The double lines in the table show change in reduction factor region.
The inelastic ADRS is shown in Figure 14.22.

R = 1 for [latex]T < T_{A}[/latex] (14.31a)

[latex]R=(2\mu -1)^{y/2}[/latex] for [latex]T_{A}< T

[latex]R=(2\mu-1)^{0.5} ext{for} T_B\lt T\lt T_C^{\prime}[/latex] (14.31c)

[latex]R=(T/T_C)\mu ext{for} T_C^{\prime}\lt T\lt T_C[/latex] (14.31d)

[latex]R=\mu ext{for} T\gt T_C [/latex] (14.31e)

[latex]\gamma =\frac{\log\left\lgroup\frac{T}{T_A} ight group }{\log \left\lgroup\frac{T_B}{T_A} ight group } [/latex] (14.31f)

[latex]S_{ ext{d inelastic}} =µ S_{ d inelastic}/R[/latex] for [latex] T

[latex]S_{ ext{d inelastic}} =S_{ d inelastic}[/latex] for [latex] T >T_{C}[/latex] (14.32b)

Table 14.8 calculations for R, [latex]S_{a}[/latex] and [latex]S_{d}[/latex] coordinates

µ = 1			µ = 1.5			µ = 2
[latex]S_{a}[/latex]/g	T(sec)	[latex]S_{d}[/latex] (cm)	[latex]R_{y}[/latex]	[latex]S_{a}[/latex]/g	[latex]S_{d}[/latex] (cm)	[latex]R_{y}[/latex]	[latex]S_{a}[/latex]/g	[latex]S_{d}[/latex] (cm)
1	0.01	0.002	1	1	0	1	1	0
1	0.03	0.022	1	1	0.03	1	1	0.04
2.71	0.125	1.053	1.41	1.92	1.12	1.73	1.56	1.22
2.71	0.2	2.696	1.41	1.92	2.86	1.73	1.56	3.11
2.71	0.25	4.213	1.41	1.92	4.47	1.73	1.56	4.86
2.71	0.3	6.067	1.41	1.92	6.43	1.73	1.56	7.01
2.71	0.35	8.258	1.41	1.92	8.76	1.73	1.56	9.54
2.71	0.4	10.785	1.41	1.92	11.44	1.73	1.56	12.45
2.71	0.45	13.65	1.41	1.92	14.48	1.8	1.51	15.17
2.71	0.5	16.852	1.50	1.81	16.85	2.00	1.36	16.85
2.3	0.6	20.596	1.50	1.53	20.60	2.00	1.15	20.6
1.95	0.7	23.767	1.50	1.30	23.77	2.00	0.98	23.77
1.77	0.8	28.178	1.50	1.18	28.18	2.00	0.89	28.18
1.6	0.9	32.237	1.50	1.07	32.24	2.00	0.80	32.24
1.5	1	37.311	1.50	1.00	37.31	2.00	0.75	37.31
1	1.5	55.967	1.50	0.67	55.97	2.00	0.5	55.97
0.7	2	69.648	1.50	0.47	69.65	2.00	0.35	69.65
0.55	2.5	85.505	1.50	0.37	85.51	2.00	0.28	85.51
0.45	3	100.741	1.50	0.30	100.74	2.00	0.23	100.74

Question 14.4: Construct an ADR spectrum for ductility ratio of 1, 1.5, 2, ...

Related Answered Questions

Re-do Example 14.5 and locate the performance point using the EC8-Part 1 method. ...

Verified Answer:

Re-do Example 14.6 and locate the performance point using the EC8-Part 1 method. ...

Verified Answer:

A SDOF system has the following data: Mass = 100 kg, Damping = 5%, Yield strength = 175 N Maximum ground acceleration = 0.25 g Locate the performance point using the ground motion of Example 14.4, if the period is 0.3 sec and capacity curve is bi-linear. ...

Verified Answer:

A SDOF system has the following data: Mass = 100 kg, Damping = 5%, Yield strength = 197 N Maximum ground acceleration = 0.25 g. Locate the performance point using the ground motion of Example 14.4, if the period is 1 sec and capacity curve is bi-linear. ...

Verified Answer:

A 10-storey RC building is shown in Figure 14.28. One of its inner frames is subjected to nonlinear static pushover analysis as well as nonlinear time-history analysis under the El Centro earthquake of May 1940. Determine the target displacement and ductility demands in various members. ...

Verified Answer:

Verified Answer:

Draw the response spectrum curves of IS:1893 code on hard soil for 2% and 5% damping in ADRS format. ...

Verified Answer:

Generate a moment-curvature curve for a concrete section shown in Figure 14.15 using the Mander model for confined concrete. ...

Verified Answer:

Generate moment-curvature curve for a reinforced concrete unconfined section is shown in Figure 14.13. ...

Verified Answer: