Question 17.28: Determine reactions of both roller–bearing for given compoun...
Determine reactions of both roller–bearing for given compound beam arrangement as shown in Fig. 17.31 by using the principles of virtual work.
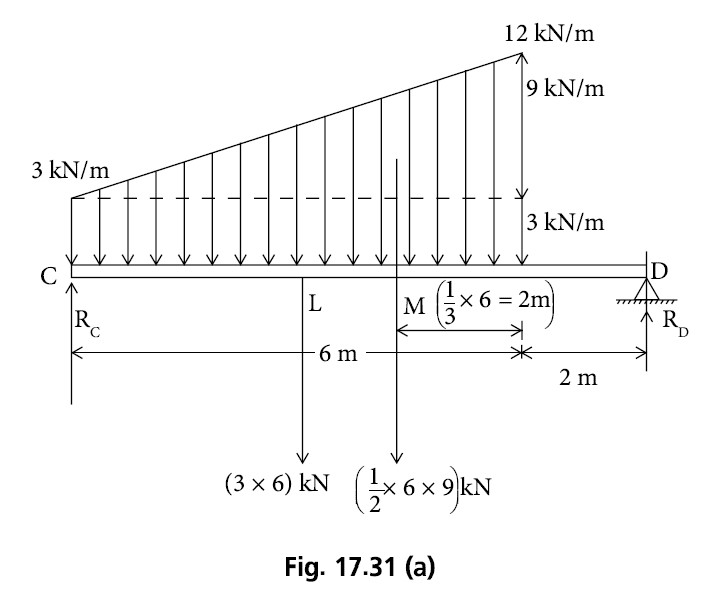
Consider free body diagram of beam CD as shown in Fig. 17.31(a). The given load is a combination of UDL and UVL intensities of 3 kN/m and 9 kN/m, respectively.
Using principles of virtual work,
R _{ C } \cdot(+\delta y)_{C}+18 \cdot(-\delta y)_{ L }+27 \cdot(-\delta y)_{ M }=0
R _{ C } \cdot(\delta y)_{C}-18 \cdot(\delta y)_{ L }-27 \cdot(\delta y)_{ M }=0 ….. (1)
From right angle triangles of Fig. 17.31 (b),
\delta \theta=\frac{(\delta y)_{C}}{8}=\frac{(\delta y)_{L}}{5}=\frac{(\delta y)_{M}}{4}
Substituting the virtual distance in equation (1),
R _{c} \cdot(8 . \delta \theta)-18(5 . \delta \theta)-27(4 . \delta \theta)=0
R _{c} =24.75 kN
Consider free body diagram of beam AB as shown in Fig. 17.31 (c)
Using the principle of virtual work,
R _{ A } \cdot(+\delta y)_{ A }+24.75(-\delta y)_{ C }=0
R _{ A } \cdot(\delta y)_{ A }-24.75 .(\delta y)_{ C }=0 ….. (2)
From right–angled triangles,
\delta \theta=\frac{(\delta y)_{A}}{5}=\frac{(\delta y)_{C}}{3}
(\delta y)_{A}=5 . \delta \theta,(\delta y)_{C}=3 . \delta \theta
Substituting the virtual distance in equation (2),
R _{ A } \cdot(5 . \delta \theta)-24.75(3 . \delta \theta)=0
R _{ A } =14.85 kN
