Question 3.SP.6: Determine the components of the single couple equivalent to ...
Determine the components of the single couple equivalent to the two couples shown.
STRATEGY: Look for ways to add equal and opposite forces to the diagram that, along with already known perpendicular distances, will produce new couples with moments along the coordinate axes. These can be combined into a single equivalent couple.
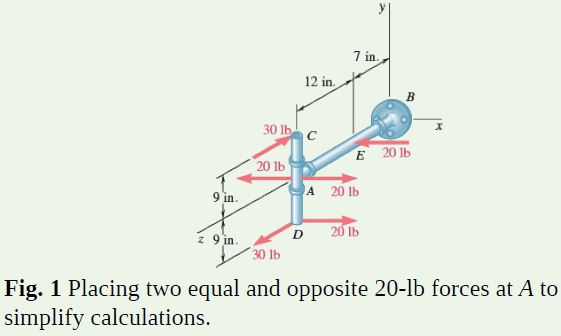
MODELING: You can simplify the computations by attaching two equal and opposite 20-lb forces at A (Fig. 1). This enables you to replace the original 20-lb-force couple by two new 20-lb-force couples: one lying in the zx plane and the other in a plane parallel to the xy plane.
ANALYSIS: You can represent these three couples by three couple vectors \pmb{M}_x, \pmb{M}_y, and \pmb{M}_z directed along the coordinate axes (Fig. 2). The corresponding moments are
M_x = −(30 lb)(18 in.)= −540 lb⋅in.
M_y = +(20 lb)(12 in.)= +240 lb⋅in.
M_z = +(20 lb)(9 in.)= +180 lb⋅in.
These three moments represent the components of the single couple M equivalent to the two given couples. You can write M as
M = −(540 lb⋅in.) i +(240 lb⋅in.) j +(180 lb⋅in.) k
REFLECT and THINK: You can also obtain the components of the equivalent single couple M by computing the sum of the moments of the four given forces about an arbitrary point. Selecting point D, the moment is (Fig. 3)
M = \pmb{M}_D =(18 in.) j ×(−30 lb)k +[(9 in.)j −(12 in.)k]×(−20 lb)i
After computing the various cross products, you get the same result, as
M = −(540 lb⋅in.) i +(240 lb⋅in.) j +(180 lb⋅in.) k
